4  Categoryทั้งเล็กและใหญ่ (Draft)

คุณสามารถที่จะเห็นประโยชน์ของcategoryต่างๆโดยการศึกษาตัวอย่างที่หลากหลายของมัน categoryมาในทุกรูปแบบและขนาดและมักจะโผล่ขึ้นมาในที่ที่ไม่คาดถึง เราจะมาเริ่มจากบางอย่างที่เรียบง่ายมากๆ

4.1 ไม่มีวัตถุอยู่

categoryที่ตรงตัวที่สุดคือตัวที่ไม่มีวัตถุอยู่เลยและดังนั้นจึงไม่มีmorphismอยู่เลย มันเป็นcategoryที่น่าเสร้าในตัวมันเองแต่มันอาจจะมีความสำคัญในบริบทของcategoryอิ่นๆ ตัวอย่างเช่น อยู่ในcategoryของทุกๆcategory(แน่นอนว่ามันมีอยู่) ถ้าคุณคิดว่าsetว่างนั้นสมเหตุสมผล แล้วทำไมจึงไม่มีcategoryว่างจึงไม่ละ

4.2 Graphอย่างง่าย

คุณสามารถที่จะสร้างcategoryโดยการแค่ต่อวัตถุต่างเข้าด้วยกันโดยลูกศร คุณสามารถที่จะจินตนาการโดยเริ่มด้วยgraphที่ระบุทิศทาง (directed graph) และทำมันให้เป็นcategoryโดยนำลูกศรมาเพิ่ม อย่างแรกทำการเพิ่มลูกศร identity แล้วก็ในทุกๆลูกศรสองตัวที่ปลายของตัวหนึ่งตรงกับจุดเริ่มต้นของอีกอัน (หรือในอีกคำหนึ่งลูกศรสองตัวที่สามารถประกอบกันได้(composable)) เราก็จะต้องเพิ่มลูกศรเข้ามาในฐานะการประกอบกันของพวกมัน ในทุกๆครั้งที่คุณเพิ่มลูกศรใหม่เข้ามาคุณก็จะต้องพิจารณาการประกอบของมันกับลูกศรอื่นๆด้วย (ยกเว้นสำหรับลูกศร identity) และกับตัวมันเอง คุณจะมักที่จะมีจำนวนลูกศรmujไม่จำกัดแต่นั่นก็ไม่เป็นไร

ในอีกวิธีในการมองของกระบวนการนี้คือคุณกำลังสร้างcategoryที่มีวัตถุเป็นทุกๆจุดในgraphและลำดับต่อๆกัน(chain)ของการเชื่อมที่ สามารถประกอบกันได้ของgraphในฐานะmorphisms (คุณสามารถที่จะคิดว่าmorphism identityในการเชื่อมกันที่มีความยาวเป็นศูนย์)

categoryแบบนี้จะถูกเรียกว่าcategory อิสระ (free) ที่ถูกสร้างมาจากgraphที่ให้มา นี่คือตัวอย่างของการสร้างแบบอิสระ (free construction) ที่เป็นกระบวนการในการทำให้โครงสร้างที่มีอยู่แล้วสมบูรณ์ขึ้นโดยการขยายมันด้วยจำนวนชิ้นที่น้อยที่สุดเพื่อที่จะให้เป็นไปตามกฎของมัน (ในที่นี้คือฎของcategory) เราจะเห็นตัวอย่างนี้มากขึ้นในอนาคต

4.3 Orders (ลำดับ)

และในตอนนี้มีไว้สำหรับอะไรบางอย่างที่แตกต่างออกไปอย่างสิ้นเชิง categoryที่morphismคือความสัมพันธ์ระหว่างobjectในที่คือความสัมพันธ์ของความน้อยกว่าหรือเท่ากับ เรามาลองตรวจสอบดูว่ามันคือcategoryจริงๆหรือไม่ เรามีmorphism identityหรือเปล่า? ทุกๆวัตถุนั้นน้อยกว่าหรือเท่ากับตัวเอง (จริง) เรามีการประกอบกันหรือเปล่า? ถ้า \(a\le b\)และ\(b\le c\)ดังนั้น\(a\le c\) (จริง) แล้วการประกอบกันที่เปลี่ยนหมู่ได้หรือเปล่า (ได้) setที่มีความสัมพันธ์แบบนี้จะถูกเรียกว่า preorder แล้วก็preorderก็เป็นcategory

คุณสามารถที่จะมีความสัมพันธ์ที่เคร่งครัดมากกว่าที่ไปตามเงื่อนไขที่มากขึ้น นั่นก็คือถ้า \(a\le b\)และ\(b\le a\)แล้ว\(a\)ต้องเหมือนกับ\(b\) สิ่งนี้ที่มีเงื่อนไขที่มากขึ้นจะถูกเรียกว่า partial order

สุดท้ายแล้วคุณสามารถที่จะกำหนดเงื่อนไขที่ว่าในวัตถุสองอย่างอย่างไรก็ได้ต้องอยู่ในความสัมพันธ์ ระหว่างกันไม่ว่าทางใดทางหนึ่งก็ตามก็นำไปสู่linear orderหรือtotal order

เรามาลองบรรยายลักษณะของsetที่เป็นลำดับในฐานะcategory ที่ที่preorderคือcategoryที่มีmorphismไม่มากกว่าหนึ่งที่มาจากวัตถุ\(a\)ตัวไหนก็ได้ไปยังวัตถุ\(b\)ตัวไหนก็ได้ อีกชื่อหนึ่งสำหรับcategoryแบบนี้คือ “บาง” (thin) preorderนั้นคือcategoryที่บาง

setของmorphismจากวัตถุ\(a\)ไปยังวัตถุ\(b\)ในcategory\(\textbf{C}\)จะถูกเรียกว่าhom-setและจะถูกเขียนว่า\(\textbf{C}(a,b)\) (หรือในบางครั้ง\(\mathbf{Hom}_{\textbf{C}}(a, b)\)) ดังนั้นทุกๆhom-setในpreorderก็จะเป็นแค่setว่างหรือsetที่มีสมาชิกเพียงตัวเดียว นี่ก็รวมถึงhom-set\(\textbf{C}(a,a)\) ที่เป็นsetจาก\(a\)ไปยัง\(a\)ที่จำเป็นที่จะเป็นsetที่มีสมาชิกเพียงตัวเดียวอย่างidentityในpreorderใดๆก็ตาม แต่คุณอาจจะมีวงจร(cycle)ในpreorder แต่วงจรจะไม่มีอยู่ในpartial order

มันเป็นสิ่งสำคัญที่จะเห็นpreorder partial orderและtotal orderเพราะว่าalgorthmในการเรียงลำดับอย่าง quicksort, bubble sort, merge sort และอื่นๆ สามารถที่จะทำงานได้อย่างถูกต้องแค่ในtotal order และpartial orderสามารถที่จะถูกเรียงลำดับผ่านการเรียงลำดับแบบtopological

4.4 Monoid ในฐานะ Set

Monoidเป็นconceptที่ง่ายมากๆแต่เป็นสิ่งที่ทรงพลังอย่างไม่น่าเชื่อ มันคือแนวคิดภายใต้เลขคณิตพื้นฐาน ทั้งการบวกและคูณนำไปสู่monoid monoidนั้นอยู่ในทุกที่ของการเขียนโปรแกรม มันโผล่ขึ้นมาในฐานะstring, list, data structuresที่foldได้ (foldable data structures), futuresในการเขียนโปรแกรมแบบconcurrent, event ในการเขียนโปรแกรมแบบfunctionalที่ตอบสนองได้(functional reactive programming)และอื่นๆ

ตามประเพณีแล้ว monoidถูกนิยามในฐานะsetที่มีการคำนวณ(operation)แบบbinary (ก็คือนำค่าสองค่ามาคำนวณรวมกัน) สิ่งที่จำเป็นจากการคำนวณนี้คือว่ามันต้องมีคุณสมบัติของการเปลี่ยนหมู่ (associativity) และมีสมาชิกที่พิเศษที่ทำตัวเหมือนunitของารคำนวณนั้นๆ

ตัวอย่างเช่น จำนวนธรรมชาติที่มีเลขศูนย์เป็นmonoidภายใต้การบวกกัน คุณสมบัติการเปลี่ยนหมู่คือการที่ว่า

\[ (a + b) + c = a + (b + c) \]

(ในอีกความหมายหนึ่งก็คือเราสามารถที่จะละวงเล็บในการบวกกันได้)

สมาชิกที่เป็นnaturalคือเลขศูนย์ก็เพราว่า

\[ 0+a=a \]

และ

\[ a+0=a \]

สมการที่สองนั้นซ้ำซ้อนก็เพราะว่าการบวกกันนั้นมีคุณสมบัติการสลับที่ (associative, \(a+b=b+a\)) แต่คุณสมบัติการสลับที่ไม่ได้อยู่ในนิยามของmonoid ยกตัวอย่างเช่นการเชื่อมต่อกันของstringนั้นไม่มีคุณสมบัติการสลับที่แต่ก็เป็นmonoid สมาชิกnaturalของการเชื่อมต่อกันของstringก็คือstringว่างที่สามารถที่จะผูกติดกับstringข้างไหนก็ได้ในแบบที่ไม่เปลี่ยนแปลงstringมันเอง

ในHaskellเราสามารถที่จะนิยามclassของtypeสำหรับmonoidsได้ เป็นtypeที่มีสมาชิกnaturalที่เรียกว่าmempty และ การคำนวณแบบbinaryที่เรียกว่าmappend

class Monoid m where
  mempty :: m
  mappend :: m -> m -> m

ในsignatureของtypeสำหรับfunctionที่มีargumentสองอย่าง m->m->m อาจจะดูแปลกในตอนแรก แต่มันจะสามารถเข้าใจได้หลังจากที่เราเข้าใจเกี่ยวกับการcurry คุณอาจจะตีความsignatureที่มีลูกศรหลายอันในสองแบบง่ายๆ ในฐานะfunctionที่มีหลายargumentsโดยที่มีtypeด้านขวาสุดเป็นtypeที่จะโดนคืน หรือในฐานะfunctionที่มีargumentอย่างหนึ่ง (ในด้านช้ายสุด)และคืนfunctionออกมา ในการตีความอย่างหลังอาจจะถูกทำให้ชัดเจนมากขึ้นโดยการเพิ่มวงเล็บเข้ามา (ที่ก็อาจจะซ้ำซากเพราะลูกศรนั้นมีคุณสมบัติการเปลี่ยนหมู่ด้านขวา) ในแบบว่าที่ว่า m->(m->m) เราจะกลับมาในการตีความแบบนี้ในอีกไม่ช้า

อาจจะสังเกตว่าในHaskellไม่มีวิธีการที่จะแสดงคุณสมบัติทางmonoidของmempty และ mappend (ก็คือความจริงที่ว่าmemptyนั้นเป็นnaturalและmappendนั้นมีคุณสมบัติการเปลี่ยนหมู่) มันคือหน้าที่ของโปรแกรมเมอร์ที่จะทำให้มั่นใจได้ว่าเงื่อนไขเหล่านี้เป็นจริง

classในHaskellไม่ได้มีความต้องการผู้เขียนสูงเมื่อเทียบกับclassต่างๆในC++ ในตอนที่คุณนิยามtypeชนิดใหม่คุณไม่จำเป็นต้องที่จะระบุclassนั้นอย่างชัดเจน คุณมีอิสระในการที่จะไม่เขียนก่อนล่วงหน้า (procrastinate) และสามารถประกาศtypeนี้ให้เป็นinstanceของclassบางclassในเวลาถัดๆไป ในฐานะตัวอย่าง เรามาประกาศStringให้เป็นmonoidโดยการที่เขียนmemptyและmappend(ที่ในความจริงแล้ว มีเขียนให้คุณอยู่แล้วในPreludeมาตรฐาน)เป็นดังต่อไปนี้

instance Monoid String where
  mempty = ""
  mappend = (++)

ในที่นี้เราได้นำการคำนวณการต่อกันของlist (++)มาใช้ช้ำได้เพราะว่าStringก็คือแค่listของตัวอักษรต่างๆ

ขออนุญาติให้ผมได้ทำการอธิบายsyntaxของHaskellว่า ในการคำนวณแบบinfixสามารถที่จะถูกเปลี่ยนให้เป็นfunctionที่มีสองargumentโดยการครอบมันด้วยวงเล็บ ถ้ามีstringสองตัวคุณสามารถที่จะต่อมันเข้ามาด้วยกันโดยการแทรก ++ ระหว่างพวกมัน

"Hello " ++ "world!"

หรือโดยการนำสองargumentsเข้ามาให้กลับการวงเล็บ (++)อย่าง

(++) "Hello " "world!"

สังเกตได้ว่าarugmentของfunctionไม่ได้แยกจากกันโดยลูกน้ำหรือถูกครอบโดยวงเล็บ (นี่อาจจะเป็นสิ่งที่ยากที่สุดในการทำความเคยชินในตอนเรียนภาษาHaskell)

แต่ก็คุ้มที่จะเน้นว่าHaskellอนุญาตให้คุณแสดงความเท่ากันของfunctionในแบบนี้

mappend = (++)

ตามแนวคิดแล้วนี้แตกต่างเมื่อเทียบกับการแสดงถึงความเท่ากันของค่าต่างๆที่ถูกผลิตโดยfunctionในตัวอย่างที่ว่า

mappend s1 s2 = (++) s1 s2

อย่างตัวแรกสามารถที่จะถูกแปลให้เป็นความเท่ากันของmorphismในcategory \(\textbf{Hask}\) (หรือ\(\textbf{Set}\)ถ้าเราจะไม่สนใจbottomที่ก็คือชื่อสำหรับการคำนวณที่ไม่มีที่สิ้นสุด) สมการแบบนี้ไม่ได้แค่มีความรวบรัดที่ไม่เยินเย้อแต่ก็สามารถถูกทำการgeneralizeในบ่อยครั้งกับcategoryอื่นๆได้ด้วย ในสิ่งอย่างหลังจะถูกเรียกว่าความเท่ากันในส่วนขยาย (extensional equality) ที่สื่อความจริงที่ว่า สำหรับทุกstringแบบไหนก็ได้ ผลลัพธ์ของ mappend และ (++)จะเหมือนกัน เนื่องด้วยว่าค่าต่างๆของargumentในบางครั้งจะถูกเรียกว่าpoints (จุด) (ในแบบที่ว่าค่าของ\(f\)ในจุดของ\(x\)) นี่เรียกว่าความเท่ากันในแต่ละจุด (point-wise equality) ความเท่ากันของfunctionโดยที่ไม่ได้ระบุถึงargumentจะถูกเรียกว่า point-free (อนึ่งสมการที่เป็นpoint-freeมักจะมีการประกอบกันของfunction ที่จะถูกเขียนด้วยสัญลักษณ์ของจุด(point)ดังนั้นนี่อาจจะเป็นสิ่งที่สับสนสำหรับผู้เริ่มต้น)

สิ่งที่ใกล้ที่สุดของการประกาศmonoidในC++อาจจะต้องใช้ feature conceptมาตราฐานของC++20อย่าง

template<class T>
struct mempty;

template<class T>
T mappend(T, T) = delete;

template<class M>
concept Monoid = requires (M m) {
    { mempty<M>::value() } -> std::same_as<M>;
    { mappend(m, m) } -> std::same_as<M>;
};

นิยามแรกคือโครงสร้างที่ควรที่จะยึดสมาชิกnaturalไว้ในทุกๆกรณี

deleteที่เป็นkeywordหมายความว่ามันไม่มีค่าเริ่มต้นถูกนิยามไว้ โดยที่มันจะถูกระบุเป็นรายกรณีไป โดยคล้ายๆกันแล้ว ก็ไม่มีค่าเริ่มต้นสำหรับ mappend

conceptของMonoid ทดสอบว่าได้มีคำนิยามที่ถูกต้องของmemepty และ mappendหรือไม่ สำหรับtypeMที่ถูกให้มา

การสร้าง(instantiation)ของconceptของMonoidสามารถที่จะมาคู่กับการเขียนการspecializationsและoverloadsที่ถูกต้อง

template<>
struct mempty<std::string> {
    static std::string value() { return ""; }
};

template<>
std::string mappend(std::string s1, std::string s2) {
    return s1 + s2;
}

4.5 MonoidในฐานะCategory

นั้นคือนิยามที่“คุ้นเคย”ของmonoidในความหมายของสมาชิกของset แต่คุณรู้ก็รู้อยู่แล้วว่าในทฤษฎีcategory เราพยายามที่จะหลีกหนีจากsetและสมาชิกของมันแล้วมาพูดเกี่ยวกับวัตถุและmorphismแทน ดังนั้นเรามาเปลี่ยนมุมมองเล็กน้อยและคิดถึงการใช้งานของoperator binaryในฐานะ”การเคลื่อน”หรือ”การขยับ”ของสิ่งต่างๆในset

ตัวอย่างเช่นการคำนวณของการบวกด้วยเลขห้าสำหรับทุกๆจำนวนธรรมชาติ มักก็จะจับคู่\(0\)ไปยัง\(5\) \(1\)ไปยัง\(6\) \(2\)ไปยัง\(7\)และต่อไปๆ นั่นคือfunctionที่ถูกนิยามในsetของจำนวนธรรมชาติ นั่นก็ดี เรามีfunctionและset โดยทั่วไปแล้วสำหรับทุกๆตัวเลข\(n\)มักจะมีfunctionของการบวก\(n\)เข้าไป (หรือก็คือตัวบวก(adder)ของ\(n\))

แล้วตัวบวกของ\(n\)จะประกอบกันอย่างไร? การประกอบกันของfunctionที่บวก\(5\)กับfunctionที่บวก\(7\)คือfunctionที่บวก\(12\) ดังนั้นการประกอบกันของตัวบวกสามารถทำให้เท่ากันได้กับกฏของการบวกกัน นั่นก็ดีเหมือนกัน เราสามารถที่จะแทนที่การบวกกันโดยการใช้การประกอบกันของfunction

แต่เดี๋ยวก่อนมันมีมากกว่านั้น ได้มีตัวบวกสำหรับสมาชิกnaturalอย่างเลขศูนย์ การบวกด้วยศูนย์ไม่ได้เคลื่อนอะไรเลยดังนั้นมันคือfunction identityในsetของจำนวนธรรมชาติ

แทนที่จะให้กฏทั่วๆไปของการบวก ผมสามารถที่จะให้กฏของการประกอบกันของตัวบวกโดยที่ไม่สูญเสียข้อมูลอะไรทั้งสิ้นเช่นกัน สังเกตว่าการประกอบกันของตัวบวกนั้นมีคุณสมบัติการเปลี่ยนหมู่ก็เพราะว่าการประกอบกันของfunctionนั้นมีคุณสมบัติการเปลี่ยนหมู่ และเรามีตัวบวกศูนย์ที่ตรงกันกับfunctionidentity

ผู้อ่านที่มีไหวพริบอาจจะเล็งเห็นว่าการจับคู่กันระหว่างจำนวนเต็มกับตัวบวกตามมาจากการเขียนแบบที่สองของsignatureของtypeของmappendว่า m->(m->m) มันบอกว่าmappend จับคู่กันของสมาชิกของsetในแบบmonoidและfunctionที่กระทำบนsetนั้น

ในตอนนี้ผมต้องการให้คุณที่จะลืมว่าคุณกำลังทำงานกับsetของจำนวนธรรมชาติและคิดเกี่ยวกับมันในฐานะวัตถุเดี่ยว เป็นชิ้นที่มีmorphismหลายอัน (ซึ่งก็คือตัวบวก) monoidคือcategoryที่มีวัตถุชิ้นเดียว ความจริงที่ว่าmonoidมาจากภาษาGreekว่าmono ที่หมายความว่าการเป็นเดี่ยว ในทุกๆmonoidสามารถที่จะถูกอธิบายในฐานะcategoryที่มีวัตถุชิ้นเดียวที่มีsetของmorphismที่อยู่ภายใต้กฏของการประกอบกัน

การต่อกันของstringก็เป็นกรณีที่น่าสนใจเพราะว่าเรามีทางเลือกของการนิยามตัวต่อกันทางในทางด้านขวา(right appenders)และตัวต่อกันทางด้านช้าย(left appendersหรือสามารถที่ถูกเรียกว่า prependerถ้าคุณต้องการ) ตารางของการประกอบกันของทั้งสองรูปแบบก็เป็นเหมือนเงากระจกสะท้อนระหว่างกัน คุณสามารถที่จะโน้มน้าวตัวเองว่าการต่อกันของ”bar”กับ”foo”นั้นตรงกันกับการต่อกันข้างหน้า (prepending)ของ “foo”หลังการต่อกันข้างหน้าของ “bar” คุณอาจจะถามว่าคำถามว่าในทุกๆmonoidที่เป็นcategory (categoryที่มีหนึ่งวัตถุ)นิยามmonoidที่เป็นsetกับoperatorที่เป็นbinaryอย่างเป็นเอกลักษณ์ได้หรือเปล่า? จริงๆแล้วเราสามารถที่จะสกัดsetออกจากcategoryที่มีหนึ่งวัตถุ setตัวนี้คือsetของmorphism (ในตัวอย่างของเราก็คือตัวบวก) ในอีกคำๆหนึ่งเรามีhom-set \(\textbf{M}(m,m)\) ของวัตถุเดี่ยว\(m\)ในcategory\(\textbf{M}\) เราสามารถที่จะนิยามoperationที่เป็นbinaryอย่างง่ายดายในsetที่ก็คือ ผลของproductแบบmonoidระหว่างสองสมาชิกในsetนั้นตรงกันกับ morphismที่เป็นเป็นการประกอบกันของสองmorphismในการทำproduct ถ้าคุณให้สมาชิกสองตัวของ\(\textbf{M}(m,m)\)ที่ตรงกันกับ \(f\)และ\(g\) productของทั้งสองจะตรงกันกับการประกอบกันของ\(f\circ g\) การประกอบนั้นเป็นไปได้ตลอดเพราะว่าสิ่งเริ่มต้นและปลายทางของmorphismเหล่านี้เป็นวัตถุเดียวกัน

และการมีกฎของการเปลี่ยนหมู่ก็อยู่ในกฎของcategory morphism identityก็คือสมาชิกnaturalของproductนี้ ดังนั้นเราสามารถที่จะ กู้setที่เป็นmonoidจากcategoryที่เป็นmonoidได้ตลอด สำหรับทุกๆความตั้งใจและวัตถุประสงค์ สองสิ่งนี้เป็นสิ่งเดียวกัน

hom-setของmonoidถูกมองในฐานะmorphismsและจุดในset

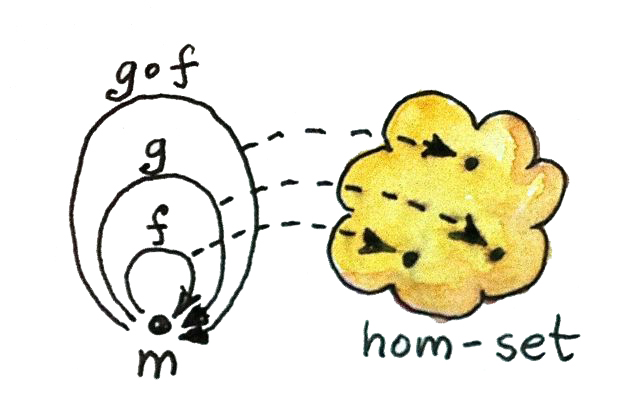
แต่ก็มีจุดเล็กน้อยที่นักคณิตศาสตร์อยากจะแย้งนั้นก็คือmorphismอาจจะไม่ก่อให้เกิดset ในโลกของcategoryได้มีสิ่งของที่ใหญ่กว่าset categoryที่morphismระหว่างสองวัตถุใดๆก็ได้ก่อให้เกิดsetจะถูกเรียกว่าlocally small ตามที่สัญญาไว้แล้วผมจะเพิกเฉยต่อรายละเอียดปลีกย่อยนี้ แต่ผมคิดว่าผมต้องกล่าวถึงเพื่อที่ให้คุณได้รู้

มีปรากฏการณ์ที่น่าสนใจหลายอย่างในทฤษฎีcategoryที่มีรากฐานในความจริงที่ว่า สมาชิกของhom-setสามารถที่จะถูกมองในฐานะทั้งmorphismที่ตามกฏของการประกอบกัน และในฐานะจุดในsetที่ในที่นี้การประกอบกันของmorphismใน\(\textbf{M}\)ถูกแปลไปสู่productแบบmonoidalในsetของ\(\textbf{M}(m,m)\)

4.6 โจทย์ท้าทาย

1. ลองสร้างcategoryที่อิสระจาก
   1. graphที่มีจุดเดียวและไม่มีตัวเชื่อม
   2. graphที่มีจุดเดียวและตัวเชื่อมอันเดี่ยวที่มีการระบุทิศทาง (ใบ้ว่า ตัวเชื่อมอันนี้สามารถที่จะถูกประกอบกับตัวมันเอง)
   3. graphที่มีจุดสองตัวและลูกศรเดี่ยวระหว่างมัน
   4. graphที่มีจุดเดี่ยวและลูกศร26อันที่มีเครื่องหมายเป็นตัวอักษรของa,b,c,…,z
2. แล้วประเภทของorderต่างๆแบบนี้คืออะไรบ้าง
   1. setของsetที่มีความสัมพันธ์แบบการอยู่ข้างในแบบที่ว่า \(A\)อยู่ใน\(B\)ถ้าทุกๆสมาชิกของ\(A\)นั้นเป็นสมาชิกของ\(B\)
   2. typeของC++ที่มาคู่กับความสัมพันธ์ของtypeย่อย T1คือtypeย่อยของT2ถ้าpointerไปยังT1สามารถที่จะผ่านเข้าไปยังfunctionที่คาดหวังกับpointerของT2โดยที่ไม่ได้นำไปสู่ปัญหาในการcompilation
3. ลองคิดว่าBoolเป็นsetที่มีค่าสองค่าTrueและFalse ลองแสดงว่ามันก่อให้เกิดmonoidสองตัว(ในทางทฤษฎีset)ที่คู่กับการคำนวณของ && (and/และ) และ || (or/หรือ)
4. ลองเขียนmonoidBoolด้วยการคำนวณแบบandในฐานะcategory ลองเขียนmorphismทั้งหมดและกฏของการประกอบกันด้วย
5. ลองเขียนการบวกกันแบบmodular \(3\) (addition modulo 3)ในฐานะcategoryแบบmonoid