10 TypeประเภทFunctions (Draft)
มาจนถึงจุดนี้ผมได้ข้ามความหมายของtypeประเภทfunctions typeประเภทfunctionนั้นมีความแตกต่างจากtypeอื่นๆ
ดูIntegerเป็นตัวอย่าง มันก็แค่setของจำนวนเต็ม Boolคือsetที่มีสองสมาชิก แต่typeแบบfunction\(a\rightarrow b\)นั้นมีมากว่านั้น มันคือsetของmorphismระหว่างวัตถุ\(a\)และ\(b\) setของmorphismระหว่างวัตถุทั้งสองในcategoryจะถูกเรียกว่าhom-set โดยที่ในcategory\(\textbf{Set}\)ทุกๆhom-setเองคือวัตถุในcategoryเช่นกัน เพราะในที่สุดแล้วมันคือset
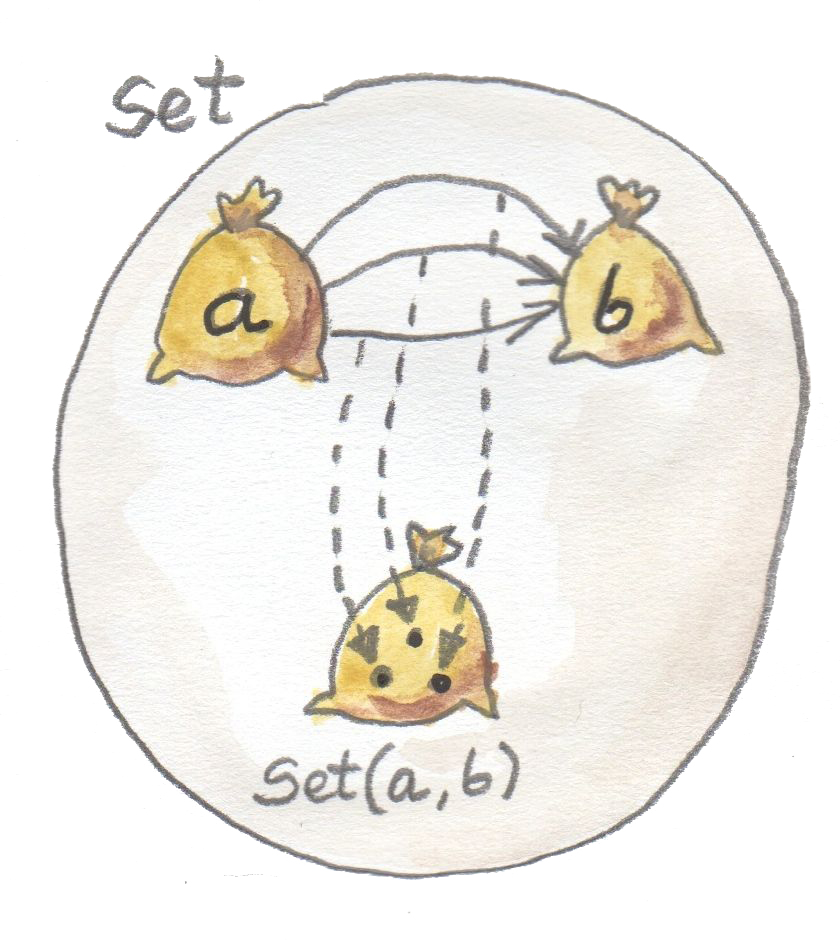
สิ่งแบบนี้ไม่จริงในcategoryอื่นๆที่hom-setนั้นอยู่ภายนอกcategory ยิ่งกว่านั้นพวกมันถูกเรียกว่าhom-setภายนอก (external hom-sets)
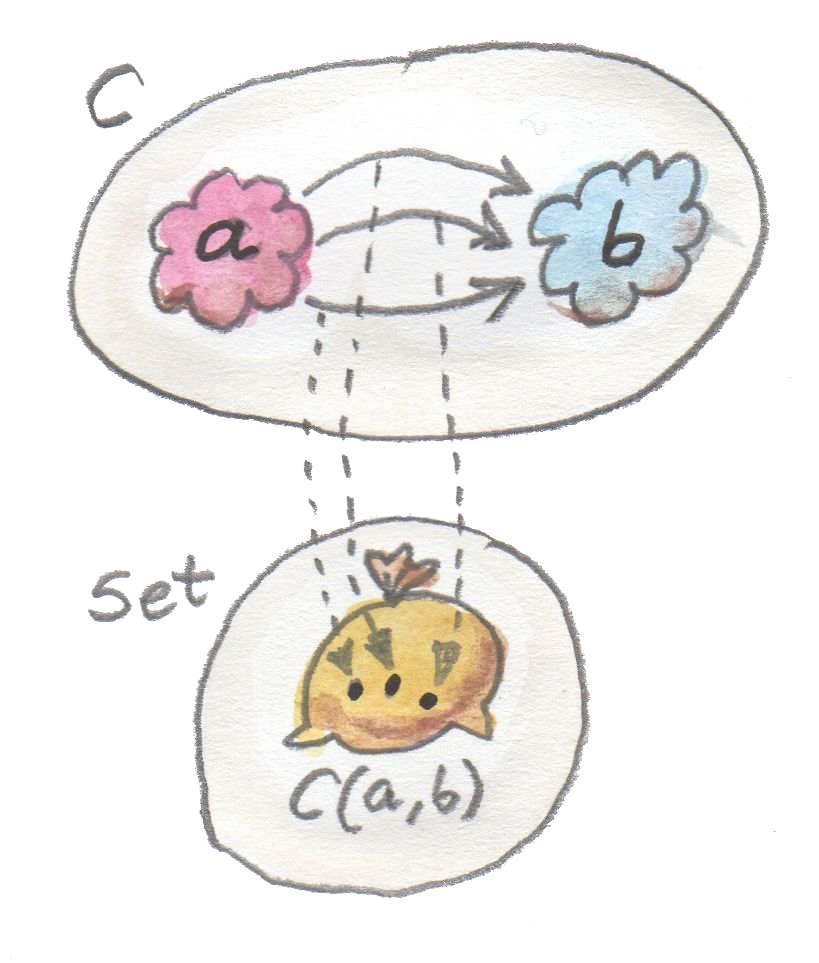
มันคือธรรมชาติในการอ้างอิงตนเองของcategory\(\textbf{Set}\) ที่ทำให้typeประเภทfunctionsมีความพิเศษ แต่มันก็มีวิธีคล้ายๆกันในการสร้างวัตถุที่แสดงแทนhom-setที่อย่างน้อยก็แยู่ในบางcategory วัตถุแบบนี้ถูกเรียกว่าhom-setภายใน (internal hom-set)
10.1 การสร้างแบบสากล (Universal Construction)
เรามาลืมสักครู่ว่าtypeประเภทfunctionsคือset และลองที่จะสร้างtypeประเภทfunctionsหรือโดยทั่วไปก็คือhom-setภายในจากศูนย์ เหมือนทุกๆครั้งไป เราจะหาทางจากcategory\(\textbf{Set}\) แต่จะหลีกเลี่ยงการใช้คุณสมบัติโดยเฉพาะของsetใดๆก็ตามอย่างระมัดระวัง เพื่อที่ว่าการสร้างนั้นจะสามารถใช้งานได้ในcategoryอื่นๆได้
typeประเภทfunctionsอาจจะถูกพิจารณาเป็นtypeประกอบ เพราะว่ามันมีความสัมพันธ์ระหว่างtypeของargumentและtypeของreturn เราได้เห็นการสร้างของtypeประกอบแล้ว ที่ที่ต้องมีความเกี่ยวข้องกับความสัมพันธ์ระหว่างวัตถุต่างๆ และได้ใช้การสร้างแบบสากลในการนิยามtypeแบบproductและcoproduct เราสามารถที่จะใช้เคล็ดลับเดียวกันในการนิยามtypeประเภทfunctions เราต้องการรูปแบบที่เกี่ยวกับสามวัตถุนี้นั้นก็คือ typeประเภทfunctionsที่เรากำลังสร้าง typeของargumentและtypeของreturn
รูปแบบที่ตรงไปตรงมาที่สุดที่ทำการเชื่อมต่อtypeทั้งสามเข้าด้วยกัน ถูกเรียกว่าการใช้งานfunction(function application)หรือการประเมิน(evaluation) ถ้ามีสิ่งที่มีคุณสมบัติของtypeประเภทfunctions ที่เราจะเรียกมันว่า\(z\) (สังเกตว่าถ้าเราไม่อยู่ในcategory\(\textbf{Set}\)สิ่งนี่ก็คือวัตถุเหมือนวัตถุอื่นๆ) และtypeของargument\(a\)(ที่เป็นวัตถุ) การใช้งานโยงคู่ๆนี้ไปยังtypeของผลลัพธ์\(b\)(ที่เป็นวัตถุ) เราได้มีวัตถุสามตัว สองในสามนั้นคงที่(ที่ก็คือเป็นตัวแทนของtypeของargumentและtypeของreturn)
เราก็จะมีการใช้งานที่ก็คือการโยง แล้วเราจะนำการโยงเหล่านี้ไปยังรูปแบบของเราได้อย่างไร? ถ้าเราได้รับอนุญาตในการมองลงไปในวัตถุต่างๆ เราสามารถจับคู่function\(f\) (ที่เป็นสมาชิกของ\(z\))กับargument\(x\)(ที่เป็นสมาชิกของ\(a\)) และโยงมันไปยัง\(fx\)(เป็นสมาชิกของ\(b\)และเป็นผลของการใช้งานของ\(f\)บน\(x\))

แต่แทนที่จะทำงานกับคู่ๆเดียว\((f,x)\) เราสามารถที่จะพูดเกี่ยวกับproductทั้งหมดของtypeประเภทfunctions\(z\)และtypeของargument\(a\)เช่นกัน product\(z\times a\)คือวัตถุและเราสามารถที่จะเลือกลูกศร\(g\)จากวัตถุนั้นไปยัง\(b\)ในฐานะmorphismในการใช้งาน ใน\(\textbf{Set}\) \(g\)อาจจะเป็นfunctionที่โยงทุกๆคู่\((f, x)\)ไปยัง\(fx\)
ดังนั้นรูปแบบ(ของเรา)คือproductระหว่างสองวัตถุ\(z\)และ\(a\) ที่ถูกต่อไปยังอีกวัตถุ\(b\) โดยmorphism\(g\)
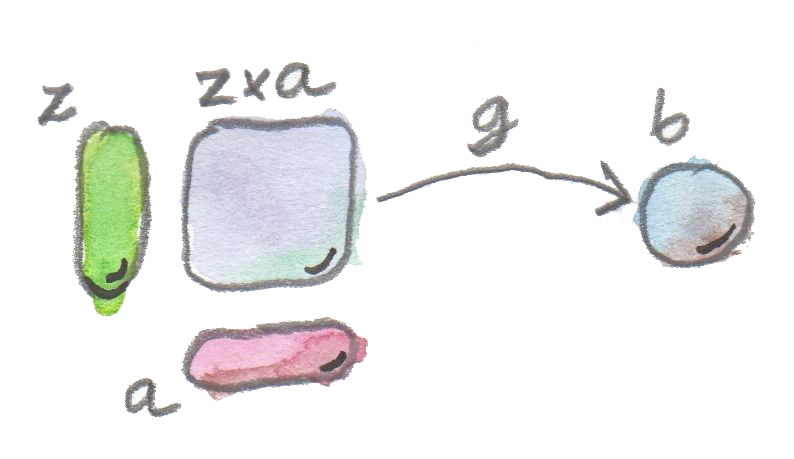
แล้วสิ่งนี้เฉพาะเจาะจงพอหรือยังในการแยกtypeประเภทfunctionsโดยการใช้การสร้างแบบสากล? ไม่ใช่ในทุกๆcategory แต่ในcategoryที่เราสนใจมันก็พอแล้ว และอีกคำถามหนึ่ง เป็นไปได้หรือเปล่าในการนิยามวัตถุประเภทfunctionsโดยที่ไม่ต้องนิยามproductก่อน? เพราะว่าเราก็มีcategoryที่ไม่มีproductหรือไม่มีproductสำหรับทุกๆคู่ของวัตถุ คำตอบคือไม่ มันไม่มีtypeประเภทfunctionsถ้าไม่มีtypeประเภทproduct เราจะกลับมาในสิ่งนี้หลังจากที่เราพูดถึงexponential
เรามาทบทวนการสร้างแบบสากล เราเริ่มจากรูปแบบของวัตถุต่างๆและmorphism นั้นคือการหาที่คลุมเครือและมักจะได้ผลลัพธ์ที่มากมาย โดยเฉพาะใน\(\textbf{Set}\)ที่แทบทุกๆอย่างนั้นต่อกับทุกๆอย่าง เราสามารถนำวัตถุอะไรก็ได้\(z\)มารวมกับ\(a\)เพื่อที่จะเป็นproductและก็จะมีfunctionจากสิ่งนี้ไปยัง\(b\)(ยกเว้นแต่\(b\)จะเป็นsetว่าง)
ดังนั้นการรที่เราใช้การจัดอันดับที่ก็เป็นอาวุธลับของเรา สิ่งนี้มักจะถูกทำโดยความต้องการที่จะมีการโยงที่เป็นเอกลักษณ์(และอันเดียว)ระหว่างวัตถุที่มีคุณสมบัติต่างๆ เป็นการโยงที่ทำการแยกตัวประกอบการสร้างของเรา ในกรณีของเราเราจะประกาศว่า\(z\)มาคู่กับmorphism\(g\)จาก\(z\times a\)ไปยัง\(b\) นั้นดีกว่า\(z\)ตัวอื่นๆที่มีการใช้งานเป็นของตนเอง\(g'\)ก็ต่อเมื่อได้มีการโยงที่เป็นเอกลักษณ์(และอันเดียว)\(h\) จาก\(z'\)ไปยัง\(z\)ในแบบที่ว่าการใช้งานของ\(g'\)แยกตัวประกอบผ่านการใช้งานของ\(g\) (คำใบ้:อ่านประโยคนี้ในขณะมองรูปๆนี้)
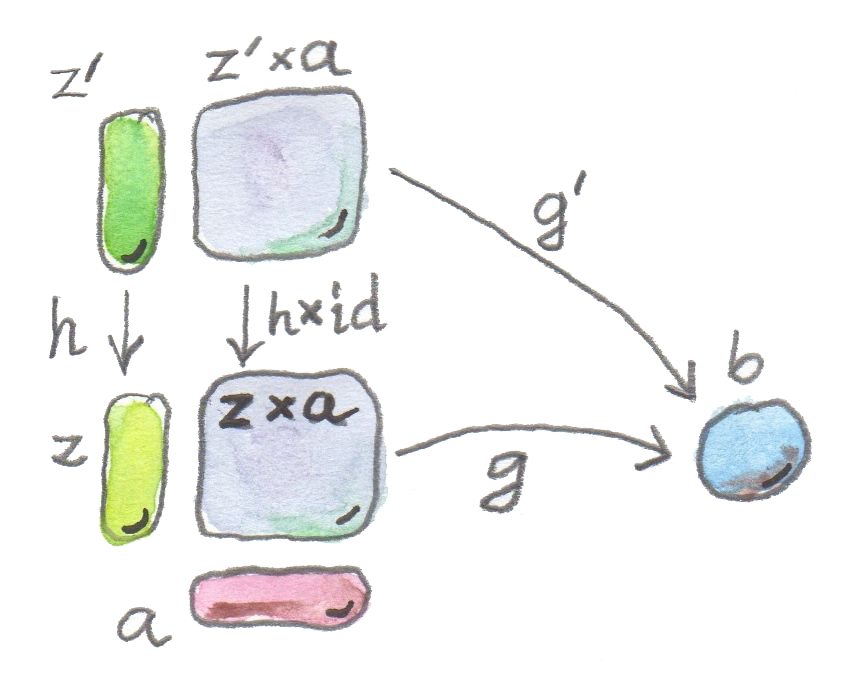
ในตอนนี้คือส่วนที่ค่อนข้างยากและคือเหตุผลหลักที่ผมเลื่อนการสร้างแบบสากลนี้ออกไปจนถึงตอนนี้ ได้มีmorphism\(h::z'\rightarrow z\)เราต้องการที่จะปิดdiagramที่มีทั้ง\(z\)และ\(z'\)คูณกับ\(a\) สิ่งที่เราต้องการจริงๆคือการโยงจาก\(z'\times a\)และ\(z\times a\)ถ้ามีการโยง\(h\)จาก\(z'\)ไปยัง\(z\) และในตอนนี้หลังจากการสนทนาของความเป็นfunctorของproductเรารู้วิธีการทำมัน เพราะว่าproductมันเองเป็นfunctor(หรือให้แม่นยำคือendo-bi-functor) มันเป็นไปได้ที่จะliftคู่ของmorphisms หรือในอีกความหมายหนึ่งเราสามารถที่จะนิยามไม่แค่productของวัตถุต่างๆแต่รวมไปถึงproductของmorphism
เนื่อด้วยว่าเราไม่ได้แตะชิ้นส่วนที่สองของproduct\(z'\times a\) เราจะทำการliftคู่ของmorphism\((h,\operatorname{id})\) ในที่นี้\(\operatorname{id}\)คือidentityของ\(a\)
ดังนั้นนี่คือวิธีการที่เราจะแยกตัวประกอบการใช้งานหนึ่งของ\(g\)จากการใช้งานของ\(g'\)
\[ g'=g\circ(h\times\operatorname{id}) \]
กุญแจสำคัญคือการกระทำของproductบนmorphism
ในส่วนที่สามคือการสร้างแบบสากลโดยการเลือกวัตถุที่ดีในสากล เรามาเรียกวัตถุนี้ว่า \(a\Rightarrow b\) (คิดถึงสิ่งนี้ในฐานะชื่อทางสัญลักษณ์สำหรับวัตถุหนึ่ง ไม่ที่จะสับสนกับ ความต้องการ(constraint)ของtypeclassของHaskell โดยที่ผมจะคุยเกี่ยวกับหลายๆวิธีในการตั้งชื่อในอีกไม่นาน) วัตถุนี้มาคู่กับการใช้งานของมันที่ก็คือmorphismจาก\((a\Rightarrow b)\times a\)ไปยัง\(b\)ที่เราจะเรียกว่าeval วัตถุ\(a\Rightarrow b\)คือสิ่งที่ดีที่สุดถ้าวัตถุอื่นที่มีคุณสมบัติสำหรับวัตถุประเภทfunctionsสามารถถูกโยงได้อย่างเป็นเอกลักษณ์(และอันเดียว) ไปยังมันในรูปแบบที่ว่าmorphismการใช้งานของมันอย่างๆ\(g\)แยกตัวประกอบผ่านeval วัตถุนี่นั้นดีกว่าวัตถุอื่นๆตามการจัดอำดับของเรา
หรือถ้าให้เป็นอย่างทางการ
วัตถุประเภทfunctionsจาก\(a\)ไปยัง\(b\)คือวัตถุ\(a\Rightarrow b\) คู่กับmorphimsอย่าง\[\operatorname{eval}::((a\Rightarrow b)\times a)\rightarrow b\]เพื่อที่ว่าสำหรับวัตถุอื่นๆที่คู่กับmorphismอย่าง\[g::z\times a\rightarrow b\]ได้มีmorphismที่เป็นเอกลักษณ์(และอันเดียว)อย่าง\[h::z\rightarrow(a\Rightarrow b)\]ที่แยกตัวประกอบ\(g\)ผ่าน\(\operatorname{eval}\) \[g=\operatorname{eval}\circ(h\times\operatorname{id})\]
แน่นอนว่าไม่มีการรับประกันว่าวัตถุอย่าง\(a\Rightarrow b\)มีอยู่สำหรับคู่ของ\(a\)และ\(b\)ใดๆก็ตามในcategoryที่ให้มา แต่มันมีอยู่ใน\(\textbf{Set}\) มากไปกว่านั้นใน\(\textbf{Set}\)วัตถุนี้นั้นisomorphicกับhom-set\(\textbf{Set}(a,b)\)
นี้คือเหตุผลในHaskellที่เราตีความtypeประเภทfunctiona -> b ในฐานะวัตถุประเภทfunctionsทางcategroy\(a\Rightarrow b\)
10.2 การCurry
เรามาดูอีกรอบในวัตถุประเภทfunctionsที่มีคุณสมบัติครบทั้งหมด แต่ในตอนนี้เรามาคิดถึงmorphism\(g\)ในฐานะfunctionที่มีสองตัวแปร\(z\)และ\(a\)
\[ g::z\times a\rightarrow b \]
การเป็นmorphismจากproductแทบจะเป็นเหมือนการเป็นfunctionที่มีสองตัวแปร โดยเฉพาะใน\(\textbf{Set}\)ที่\(g\)คือfunctionจากคู่ของค่าต่างๆ ที่หนึ่งในนั้นมาจากset\(z\)และอีกตัวที่มาจากset\(a\)
ในอีกทางหนึ่ง คุณสมบัติสากลบอกเราว่าแต่ละ\(g\)ได้มีmorphism\(h\)ที่โยง\(z\)ไปยัง วัตถุประเภทfunctionอย่าง\(a\Rightarrow b\)
\[ h::z\rightarrow\big(a\Rightarrow b\big) \]
ใน \(\textbf{Set}\)นี่หมายความว่า\(h\)คือfunctionที่นำตัวแปรเดี่ยวของtype\(z\) และคืนค่าให้เป็นfunctionจาก\(a\)และ\(b\) นั้นทำให้\(h\)เป็นfunctionที่higher order ดังนั้นการสร้างแบบสากลสร้างความตรงกันแบบหนึ่งต่อหนึ่งระหว่างfunctionที่มีสองตัวแปร และfunctionที่มีตัวแปรเดี่ยวที่คืนค่าเป็นfunction ความตรงกันนี้ถูกเรียกว่าการcurryและ\(h\)ถูกเรียกเป็นรูปแบบที่ผ่านการcurryแล้วของ\(g\)
ความตรงกันนี้เป็นแบบหนึ่งต่อหนึ่งเพราะว่าถ้ามี\(g\)ใดๆก็ตามก็จะมี\(h\)ที่เป็นเอกลักษณ์(และอันเดียว) และถ้ามี\(h\)ใดๆก็ตามคุณสามารถที่จะสร้างfunctionที่มีสองargumentใหม่โดยการใช้สูตรดังนี้
\[ g = \operatorname{eval}\circ(h\times\operatorname{id}) \]
function\(g\) สามารถถูกเรียกว่ารูปแบบของ\(h\)ที่ถูกuncurriedแล้ว
การcurryนั้นจริงๆแล้วถูกสร้างภายในsyntaxของHaskell โดยที่มีfunctionที่นำfunctionกลับมา
a -> (b -> c)ที่มักจะถูกคิดว่าเป็นfunctionที่มีสองตัวแปร นั้นคือวิธีการที่เราอ่านรูปแบบของsignatureโดยที่ไม่มีวงเล็บ
a -> b -> cการตีความนี้นั้นชัดเจนในทางที่ว่าเรานิยามfunctionที่มีหลายargument ตัวอย่างเช่น
catstr :: String -> String -> String
catstr s s' = s ++ s'ในfunctionเดียวกันก็สามารถถูกเขียนในฐานะfunctionที่มีargumentเดี่ยว ในการreturn functionในlambda
catstr' s = \s' -> s ++ s'นิยามทั้งสองนั้นเท่ากันและ ทั้งสองสามารถถูกใช้งานบางส่วนโดยแค่มีargumentตัวเดียว ได้สร้างfunctionที่มีargumentเดี่ยวในแบบที่ว่า
greet :: String -> String
greet = catstr "Hello "ถ้าให้พูดอย่างเคร่งครัดfunctionที่มีตัวแปรสองตัวคือสิ่งที่นำpair (typeประเภทproduct)
(a, b) -> cมันตรงไปตรงที่จะแปรระหว่างทั้งสองรูปแบบและทั้งสองfunction (ที่เป็นhigher order)การทำการเหล่านี้จะถูกเรียกว่าcurryและuncurry
curry :: ((a, b) -> c) -> (a -> b -> c)
curry f a b = f (a, b)และ
uncurry :: (a -> b -> c) -> ((a, b) -> c)
uncurry f (a, b) = f a bสังเกตว่าcurryคือตัวที่ทำการแยกตัวประกอบ สำหรับการสร้างแบบสากลของวัตถุประเภทfunction สิ่งนี้ชัดเจนอย่างมากถ้ามันถูกเขียนในรูปแบบนี้
factorizer :: ((a, b) -> c) -> (a -> (b -> c))
factorizer g = \a -> (\b -> g (a, b))(เตือนความจำ:ตัวที่ทำการแยกตัวประกอบสร้างfunctionที่ทำการแยกตัวประกอบ)
ในภาษาที่ไม่ใช่functionalอย่างC++การcurryนั้นเป็นไปได้แต่ไม่ตรงไปตรงมา คุณสามารถที่จะคิดถึงfunctionที่มีมากว่าหนึ่งargumentในC++ที่ตรงกันกับfunctionของHaskellที่นำtupleเข้ามา (ถึงแม้ในการทำให้สับสนมาชึ้น ในC++คุณสามารถที่จะนิยามfunctionที่นำstd::tuple รวมไปถึงfunctionแบบvariadicและfunctionที่นำlistแบบinitializerเข้ามา)
คุณสามารถที่จะใช้functionของC++ใช้templatestd::bind ตัวอย่างเช่นถ้ามีfunctionของสองstring
std::string catstr(std::string s1, std::string s2) {
return s1 + s2;
}คุณสามารถที่จะนิยามfunctionของstringตัวเดียว
using namespace std::placeholders;
auto greet = std::bind(catstr, "Hello ", _1);
std::cout << greet("Haskell Curry");Scalaที่มีความเป็นfunctionalมากกว่าC++หรือJavaตกอยู่ระหว่างทั้งสอง ถ้าคุณคาดว่าfunctionที่คุณกำลังนิยามจะถูกใช้งานเป็นบางส่วน คุณสามารถนิยามมันด้วยlistของargumentหลายๆอย่าง
def catstr(s1: String)(s2: String) = s1 + s2แน่นอนว่าสิ่งนี้จำเป็นต้องมีการคาดเดา/วางแผนล่วงหน้าของคนเขียนlibrary
10.3 Exponential
ในงานทางคณิตศาสตร์ (mathematical literature) วัตถุประเภทfunctionsหรือhom-objectภายในระหว่างสองวัตถุ\(a\)และ\(b\) มักจะถูกเรียกว่าexponentialและถูกเขียนโดย\(b^a\) สังเกตว่าtypeของargumentนั้นจะอยู่ข้างบน การเขียนรูปแบบนี้อาจจะดูแปลกในตอนแรก แต่มันมีเหตุผลที่ชัดเจนมากถ้าคุณคิดถึงความสัมพันธ์ระหว่างfunctionกับproduct เราได้เห็นแล้วว่าเราต้องใช้productในการสร้างแบบสากลของhom-objectภายใน แต่ความสัมพันธ์นั้นไปลึกกว่านั้น
มันดีที่สุดในตอนที่คุณพิจารณาfunctionระหว่างtypeจำกัด (typeที่มีจำนวนของค่าที่จำกัดอย่าง Bool Char หรือแม้กระทั้งIntหรือDouble) functionอย่างนี้ อย่างน้อยในหลักการ สามารถที่จะถูกจดจำหรือแปลงให้เป็นdata structureที่สามารถถูกค้นหาได้ และสิ่งนี้คือแก่นแท้ของความเท่ากับระหว่างfunction(ที่ก็คือmorphism)และtypeแบบfunction(ที่ก็คือวัตถุ)
ตัวอย่างเช่นในfunctionที่pureจากBoolนั้นถูกระบุได้อย่างทั้งหมดโดยคู่ของค่าต่างๆ หนึ่งในนั้นคู่กับFalseและอีกตัวหนึ่งคู่กับTrue setของfunctionที่เป็นไปได้ทั้งหมดจากBoolไปยังIntคือsetของคู่ทั้งหมกของInt นี่เหมือนกับproductInt x Intหรือในการเขียนที่สร้างสรรค์หน่อยก็จะเป็น Int^2
ในอีกตัวอย่างหนึ่ง เรามาดูที่typeของC++อย่างcharที่ประกอบด้วย256ค่า (CharของHaskellนั้นใหญ่กว่าเพราะว่าHaskellใช้Unicode) ได้มีหลายfunctionในส่วนของlibaryมาตราฐานของC++ที่มักจะถูกเขียนโดยการค้นหา functionอย่างisupperหรือisspaceถูกเขียนโดยการใช้ตาราง(table) ที่มีความเหมือนกับtupleของ256ค่าของBoolean tuple นี่คือtypeประเภทproductดังนั้นเรากำลังทำงานกับproductของBoolean 256ตัว bool x bool x bool x ... x bool เรารู้จากเลขคณิตว่าproductช้ำๆนิยามการยกกำลัง ถ้าคุณ”คูณ”boolด้วยตัวเอง256(หรือchar)ครั้ง คุณก็จะได้boolยกกำลังcharหรือbool^char
แล้วมีจำนวนเท่าไหร่ในtypeที่นิยามในแบบของtuple 256ตัวของbool นั้นคือ\(2^{256}\)เป้ะๆ นี้คือจำนวนของfunctionจากcharไปยังboolที่แตกต่างกัน ที่แต่ละfunctionนั้นคู่กับtuple 256ตัวที่เป็นเอกลักษณ์(และอันเดียว) คุณสามารถที่จะคำนวนในแบบเดียวกันว่าจำนวนของfunctionจากboolไปยังcharที่ก็คือ\(256^2\)และอื่นๆ การเขียนแบบexponentialสำหรับtypeประเภทfunctionนั้นมีเหตุผลอย่างมากในกรณีเหล่านี้
เราคงจะไม่ต้องที่จะจำfunctionจากintหรือdoubleทั้งหมด แต่ในความเท่ากันระหว่างtypeประเภทfunctionและข้อมูลก็ยังอยู่ ถึงแม้มันจะไม่สามารถใช้ได้ในความเป็นจริง ได้มีtypeที่ไม่จำกัดตัวอย่างเช่นlist, stringและtree การพยายามที่จะจำfunctionเหล่านี้จากtypeเหล่านี้อาจจะต้องใช้พื้นที่จัดเก็บไม่จำกัด Haskellนั้นเป็นภาษาที่lazy(ขี้เกียจ)ดังนั้นขอบเขตระหว่างdata structureที่ถูกประเมินอย่างlazyและfunctionนั้นไม่ชัดเจน dualityของfunctionกับข้อมูลนี้ได้อธิบายวิธีการมอง(identificaiton)ของtypeประเภทfunctionของHaskell กับวัตถุexponentialในแบบcategoryที่มีความใกล้ทางความคิดของเราต่อข้อมูล
10.4 CategoryแบบCartesian Closed
ถึงแม้ผมจะยังใช้categoryของsetในฐานะแม่แบบของtypesและfunction มันคุ้มที่จะเอ่ยถึงว่ามันมีชุดของcategoryที่ใหญ่กว่าและสามารถถูกใช้สำหรับวัตถุประสงค์นี้ categoryเหล่านี้ถูกเรียกว่าCartesian Closed โดยที่\(\textbf{Set}\)คือแค่หนึ่งในตัวอย่างของcategoryแบบนี้
categoryแบบcartesian closedต้องมี
- วัตถุสุดท้าย
- productของคู่ของวัตถุใดๆก็ตาม
- exponentialของคู่ของวัตถุใดๆก็ตาม
อยู่ ถ้าคุณพิจารณาexponentialในฐานะการทำproductช้ำๆ(อาจจะเป็นแบบไม่มีที่สิ้นสุด)แล้ว คุณสามารถที่จะคิดถึงcategoryแบบcartesian closedในฐานะสิ่งที่รองรับproductที่มีจำนวนเท่าใหร่ก็ได้ โดยเฉพาะวัตถุสุดท้ายที่สามารถถูกคิดในฐานะproductของวัตถุศูนย์ (หรือกำลังศูนย์ของวัตถุ)
สิ่งที่น่าสนใจเกี่ยวกับcategoryแบบcartesian closed จากมุมมองของวิทยาศาสตร์คอมพิวเตอร์คือมันให้modelอย่างง่ายสำหรับlambda calculusที่มีtypeแบบง่าย ที่เป็นพื้นฐานของภาษาโปรแกรมที่มีtypeทั้งหมด
วัตถุสุดท้ายและproductมีdualที่คือวัตถุเริ่มต้นและcoproduct categoryแบบcartesian closedที่ก็รองรับทั้งสอง และในที่productมีคุณสมบัติการแจกแจงเหนือcoproduct
\[ \begin{gather*} a \times (b + c) = a \times b + a \times c \\ (b + c) \times a = b \times a + c \times a \end{gather*} \]
จะถูกเรียกว่าcategoryแบบbicartesian closed เราจะเห็นในส่วนถัดไปว่าcategoryแบบbicartesian closedที่\(\textbf{Set}\) เป็นตัวอย่างเด่นนั้นมีคุณสมบัติที่น่าสนใจ
10.5 Typeประเภทข้อมูลแบบพีชคณิตและexponentials
ในการตีความของtypeแบบfunctionในฐานะexponentialนั้นเข้าได้ดีกับแบบแผนของtypeประเภทข้อมูลแบบพีชคณิต ที่กลับกลายมาเป็นว่าสมการพื้นฐานทั้งหมดจากพีชคณิตในมัธยมปลายที่โยงความสัมพันธ์ของตัวเลขศูนย์และหนึ่ง การบวก การคูณและการยกกำลัง ยังคงไว้อยู่ในcategoryแบบbicartesian closedใดๆก็ตามสำหรับ วัตถุเริ่มต้นและสุดท้าย coproduct product และexponentialตามลำดับ เรายังไม่มีเครื่องมือที่จะพิสูจน์(อย่างadjunctionหรือlemmaของYoneda) แม้กระนั้นผมจะทำรายการของพวกมันในที่นี่ในฐานะแหล่งของความเข้าใจ(intuition)ที่มีประโยชน์
10.5.1 ยกกำลังศูนย์
\[ a^0=1 \]
ในการตีความแบบcategoricalเราแทนที่\(0\)ด้วยวัตถุเริ่มต้น\(1\)ด้วยวัตถุสุดท้ายและความเท่ากันด้วยisomorphism exponetialคือhom-objectภายใน exponentialนี้แสดงแทนsetของmorphismจากวัตถุเริ่มต้นไปยังวัตถุใดๆก็ตาม\(a\) โดยความหมายของวัตถุเริ่มต้น ได้มีแค่morphismเดีี่ยวดังนั้นhom-set\(\textbf{C}(0,a)\)คือsetที่มีสมาชิกเดีี่ยว setที่มีสมาชิกเดีี่ยวคือวัตถุสุดท้ายใน\(\textbf{Set}\)ดังนั้นสมการนี้จึงถูกต้องอย่างตรงไปตรงมาใน\(\textbf{Set}\) สิ่งที่เราพูดถึงนั้นถูกต้องในbicartesian closedใดๆก็ตาม
ในHaskellเราแทนที่\(0\)ด้วยVoid \(1\)ด้วยtypeแบบunitและ exponentialด้วยtypeประเภทfunction สิ่งที่ผมเสนอคือว่าsetของfunctionจากVoidไปยังtypeaใดๆก็ตามนั้น เท่ากับtypeแบบunitที่คือtypeที่มีสมาชิกเดีี่ยว ในอีกความหมายหนึ่ง ได้มีแต่หนึ่งfunctionVoid -> a แต่เราได้เห็นfunctionนี้มาก่อน โดยที่มันถูกเรียกว่าabsurd
มันนั้นยุ่งยากเล็กน้อยในสองเหตุผล หนึ่งในนั้นคือการที่ว่าในHaskellเราไม่มีtypeที่ไม่มีอะไรอยู่เลย(uninhabited types) ในทุกๆtypeเก็บ”ผลลัพธ์ของการคำนวณที่ไม่มีที่สิ้นสุด”หรือbottom เหตุผลที่สองคือการเขียนทั้งหมดของabsurdนั้นมีความเท่ากับเพราะว่า ไม่ว่ามันจะทำอะไร ไม่มีใครที่จะสามารถใช้งานมันได้ ไม่มีค่าที่จะถูกส่งเข้าไปในabsurd (และถ้าคุณสามารถที่จะส่งการคำนวณที่ไม่มีที่สิ้นสุดมันก็จะไม่คืนค่าอะไรกลับมา)
10.5.2 ยกกำลังของหนึ่ง
\[ 1^a=1 \]
สมการนี้ในการตีความใน\(\textbf{Set}\)นำนิยามของวัตถุสุดท้ายกลับมาที่ก็คือได้มีmorphismที่เป็นเอกลักษณ์(และอันเดียว) จากวัตถุใดๆก็ตามไปยังวัตถุสุดท้าย โดยทั่วไปhom-objectภายในจาก\(a\)ไปยังวัตถุสุดท้ายนั้นisomorphicกับวัตถุสุดท้ายเอง
ในHaskellได้มีแค่functionอันเดียวจากtypeใดๆไปยังunit เราได้เห็นfunctionแล้วก่อนหน้านี้ มันถูกเรียกว่าunit คุณสามารถที่จะคิดถึงมันในฐานะfunctionconstที่ถูกใช้ในบางส่วนต่อ()
10.5.3 ยกกำลังหนึ่ง
\[ a^1 = a \]
นี่คือการนำข้อสังเกตว่าmorphismจากวัตถุสุดท้ายกสามารถถูกใช้ในการเลือก”สมาชิก”ของวัตถุaกลับมา setของmorphismแบบนี้จึงisomorphicกับวัตถุเอง ใน\(\textbf{Set}\)และHaskell ความisomorphismนั้นอยู่ระหว่างสมาชิกของsetaและfunctionที่เลือกสมาชิกเหล่านั้นคือ() -> a
10.5.4 ยกกำลังของผลบวก
\[ a^{b+c} = a^b\times a^c \]
ในทางcategoryแล้ว สิ่งนี้บอกว่าexponentialจากcoproductของสองวัตถุนั้นisomorphicกับproductของexponentialทั้งสอง ในHaskellสมการแบบพีชคณิตนี้มีการตีความที่ใช้ได้จริง มันบอกเราว่าfunctionจากผลบวกของtypeทั้งสองนั้นเท่ากับคู่ของfunctionจากแต่ละtype นี่เป็นแค่case analysisที่เราใช้ในตอนที่นิยามfunctionบนtypeแบบsum แทนที่จะเขียนนิยามของfunctionคู่กับcase เรามักจะแยกมันไปยังสองfunction(หรือมากกว่า)ที่ทำงานกับconstructorของtypeแยกๆกัน ตัวอย่างเช่นนำfunctionจากtypeแบบsumอย่าง (Either Int Double)
f :: Either Int Double -> Stringมันอาจจะถูกนิยามในฐานะคู่ของfunctionจากIntและDoubleตามลำดับ
f (Left n) = if n < 0 then "Negative int" else "Positive int"
f (Right x) = if x < 0.0 then "Negative double" else "Positive double"ในที่นี้nคือIntและxคือDouble
10.5.5 ExponentialsของExponentials
\[ (a^b)^c = a^{b\times c} \]
นี่คือแค่วิธีการของการแสดงถึงการcurryในรูปแบบของวัตถุexponentialจริงๆ functionที่return functionกลับมานั้นเท่ากับfunctionจากproduct (ซึ่งก็คือfunctionที่มีargumentสองตัว)
10.5.6 Exponentialsบนproduct
\[ (a\times b)^c = a^c\times b^c \]
ในHaskell functionที่ทำการreturn pairกลับมานั้นมีความเท่ากันกับคู่ของfunctionที่แต่ละตัวสร้างสมาชิกของคู่ที่ให้มา
มันค่อนข้างที่จะเหลือเชื่อวิธีการที่สมการที่เรียบง่ายของพีชคณิตระดับมัธยม สามารถถูกยกไปยังทฤษฎีcategoryและมีการใช้งานได้ในความเป็นจริงในการเขียนโปรแกรมแบบfunctional
10.6 IsomorphismของCurry-Howard
ผมได้พูดถึงแล้วเกี่ยวกับความตรงกันของtypeข้อมูลประเภทlogicและพีชคณิต typeVoid และtypeของunitอย่าง()ตรงกันกับfalseและtrue typeแบบproductและtypeแบบsumตรงกันกับconjunctionทางตรรกศาสตร์\(\wedge\) (AND, และ) และdisjunction\(\vee\)(OR, หรือ) ในแบบแผนนี้typeประเภทfunctionที่เราได้ทำการนิยาม จะตรงกันกับimplicationทางตรรกศาสตร์\(\Rightarrow\) ในอีกความหมายหนึ่ง typea -> bสามารถถูกเรียกในฐานะว่า”ถ้า\(a\)แล้ว\(b\)”
ตามมาจากisomorphismของCurry-Howard ทุกๆtypeสามารถถูกตีความในฐานะproposition (คือstatementหรือการตัดสินที่อาจจะเป็นจริงหรือไม่) propositionแบบนี้นั้นถูกพิจารณาว่าจริงถ้าtypeนั้นมีสมาชิกอยู่และไม่จริงถ้ามันไม่มี โดยเฉพาะการที่implicationทางตรรกศาสตร์นั้นมีค่าเป็นจริงถ้ามีtypeแบบfunctionที่ตรงกับมันมีสมาชิกอยู่ นั้นหมายความว่าได้มีfunctionของtypeนั้นอยู่ การเขียนของfunctionนั้นจึงเป็นการพิสูจน์ของทฤษฎีบท นั้นก็คือการเขียนโปรแกรมนั้นจึงเท่ากันกับการพิสูจน์ทฤษฎีบท เรามาดูในบางตัวอย่าง
เรานำfunctionevalที่เราได้นำมาในนิยามของวัตถุประเภทfunction โดยที่signatureของมันคือ
eval :: ((a -> b), a) -> bมันนำคู่ที่ประกอบด้วยfunctionและargumentของมัน และสร้างผลลัพธ์ที่มีtypeที่ถูกต้อง นี่คือการเขียนในHaskellของmorphismนี้
\[ \operatorname{eval} :: (a \Rightarrow b) \times a \to b \]
ที่นิยามtypeประเภทfunction\(a\Rightarrow b\)(หรือคือวัตถุexponentialอย่าง\(b^a\)) เรามาแปลsignatureไปยังpredicateทางตรรกศาสตร์โดยการใช้isomorphismของCurry-Howard
\[ ((a \Rightarrow b) \wedge a) \Rightarrow b \]
นี่คือวิธีการที่คุณสามารถอ่านtype\(a\Rightarrow b\)คือถ้ามันเป็นจริงก็หมายความว่า\(b\)ตามมาจาก\(a\) และถ้า\(a\)เป็นจริงแล้ว\(b\)ต้องเป็นจริง มันมีเหตุผลมากและสามารถทำความเข้าใจได้ สิ่งนี้รู้จักในฐานะmodus ponensตั้งแต่สมัยโบราณแล้ว เราสามารถพิสูจน์ทฤษฎีบทนี้โดยการเขียนfunctionออกมาว่า
eval :: ((a -> b), a) -> b
eval (f, x) = f xถ้าคุณให้คู่ที่ประกอบด้วยfunctionfที่นำaเข้ามาและคืนค่าเป็นbและค่าจริงๆอย่างxของtypea ผมสามารถที่จะสร้างค่าจริงๆที่อยู่ในtypebโดยการแค่ใช้งานfunctionfกับx โดยการเขียนfuncionนี้ผมได้แสดงว่าtype((a -> b), a) -> b นั้นมีสมาชิกอยู่ ดังนั้นmodus ponensนั้นจริงในlogicของเรา
แล้วถ้าเป็นprediateที่ไม่จริงอย่างชัดเจน? ตัวอย่างเช่นถ้า\(a\)หรือ\(b\)นั้นจริงแล้ว\(a\)ต้องเป็นจริง
\[ a \vee b \Rightarrow a \]
สิ่งนี้ไม่จริงอย่างชัดเจนเพราะว่าคุณสามารถเลือก\(a\)ที่ไม่จริงและ\(b\)ที่จริงและนี่คือตัวอย่างขัดแย้ง(counter-example)
ในการโยงpredicateนี้ไปยังsignatureของfunctionโดยการใช้ isomorphismของCurry-Howardเราก็จะได้
Either a b -> aลองเขียนยังไงก็ตามคุณจะไม่สามารถที่จะเขียนfunctionนี้ได้ คุณไม่สามารถที่จะสร้างค่าของtypeaถ้าคุณเรียกด้วยค่าของRight (จำไว้ว่าเรากำลังพูดถึงfunctionที่pure)
สุดท้ายแล้วเรา(กลับ)มาที่ความหมายของfunctionabsurd
absurd :: Void -> aลองพิจารณาว่าVoidแปลไปยังfalseเราก็จะมี
\[ \operatorname{false}\Rightarrow a \]
ทุกๆอย่างตามมาจากความไม่จริง(Anything follows from falsehood/ex falso quodlibet) นี่คือหนึ่งในการพิสูจน์(เขียน)ของstatementนี้(function)ในHaskell
absurd (Void a) = absurd aที่ที่Voidถูกนิยามว่า
newtype Void = Void Voidเหมือนในทุกครั้งtypeVoidนั้นมีความชับช้อน นิยามนี้ทำให้มันเป็นไปไม่ได้ที่จะสร้างบางค่าเพราะว่าในการสร้างค่าๆหนึ่งคุณต้องให้ค่าๆหนึ่งกับมัน ดังนั้นfunctionabsurdไม่สามารถที่จะถูกเรียก
ได้มีตัวอย่างที่น่าสนใจมากมาย แต่ก็มีด้านที่ใช้งานได้จริงของisomorphismของCurry-Howardจริงหรือเปล่า? อาจจะไม่ในการเขียนโปรแกรมทั่วๆไป แต่ได้มีภาษาโปรแกรมอย่างAgdaหรือCoqที่ใช้ข้อได้เปรียบของisomorphismของCurry-Howardในการพิสูจน์ทฤษฎีบท
คอมพิวเตอร์ไม่ได้แค่ช่วยนักคณิตศาสตร์ในการทำงานของพวกเขา มันได้ปฏิวัติรากฐานของคณิตศาสตร์ ในหัวข้อการวิจัยที่มาแรงในด้านที่เรียกว่าHomotopy Type Theory และการทฤษฎีtypeที่ตามมาและได้ผลประโยชน์ มันเต็มไปด้วย Booleans, integers, products coproducts typeประเภทfunctionและอื่นๆ และในการที่จะขจัดความสงสัยใน ทฤษฎีบทได้ถูกเขียนในCoqและAgda คอมพิวเตอร์นั้นกำลังปฏิวัติโลกใบนี้มากกว่าหนึ่งแบบ
10.7 บรรณานุกรม
- Ralph Hinze, Daniel W. H. James, Reason Isomorphically! 1 (จงเหตุผลแบบisomorphic!) บทความนี้มีการพิสูจน์ของสมการพีชคณิตในมัธยมเหล่านี้ในทฤษฎีcategoryที่ผมเอ่ยถึงในบทนี้