29 Categoryที่ถูกเพิ่มค่า(Enriched Categories) (Sketch)

Categoryนั้นมีขนาดเล็กถ้าวัตถุของมันก่อให้เกิดset แต่เรารู้ว่าได้มีสิ่งที่ใหญ่กว่าset โดนเฉพาะเช่นsetของsetทั้งหมดไม่สามารถถูกสร้างภายในทฤษฎีsetทั่วไป(ทฤษฎีของZermelo-Fraenkelที่สามารถเพิ่มเติมด้วยสัจพจน์การเลือก) ดังนั้นcategoryของsetทั้งหมดต้องใหญ่ ได้มีเทคนิคอย่างจักรวาลของGrothendieckที่สามารถถูกใช้ในการนิยามชุดที่ไปยิ่งกว่าsets เทคนิคเหล่านี้ให้เราได้พูดเกี่ยวกับcategoryขนาดใหญ่ต่างๆ

categoryที่มีขนาดเล็กเฉพาะแห่ง(locally small)ถ้าmorphismsระหว่างสองวัตถุใดๆก็ตามก่อให้เกิดset ถ้าพวกมันไปม่ก่อเป็นset เราต้องคิดบางนิยามใหม่ โดยเฉพาะเช่น มันมายความว่าอะไรในการประกอบmorphismถ้าเราไท่สามารถเลือกพวกมันจากset? วิธีแก้คือการที่เราต้องbootstrapพวกเราเองโดยการแทนที่hom-setsที่คือวัตถุต่างๆใน$\textbf{Set}$ที่วัตถุต่างๆจากสมาชิกบางcategoryอื่นๆ$\textbf{V}$ ความแตกต่างคือว่า โดนทั่วไปแล้ววัตถุนั้นไม่มีสมาชิก ดังนั้นเราจึงไม่สามารถที่จะพูดเกี่ยวกับmorphismเดี่ยวๆได้อีกต่อไป เราต้องนิยามคุณสมบัติทั้งหมดของcategoryที่ถูกเพิ่มค่าในรูปแบบของการดำเนินงานที่สามารถใช้การดำเนินการบนhom-objectsโดยรวม ในการที่จะทำแบบนั้น categoryที่ให้hom-objectsต้องมีโครงสร้างเสริม(มันต้องเป็นcategoryแบบmonoid) ถ้าเราเรียกcategoryแบบmonoidนี้ว่า$\textbf{V}$ เราสามารถพูดเกี่ยวกับcategory$\textbf{C}$ที่ถูกเพิ่มค่าข้างบน$\textbf{V}$

นอกเหนือจากเหตุผลทางขนาก เราอาจจะมีความสมใจในการgeneralizeของhom-setsไปยังบางอย่างที่มีโครงสร้างมากกว่าแค่sets ตัวอย่างเช่น categoryแบบดั้งเดิมไม่มีนวคิดของระยะทางระหว่างวัตถุ สองวัตถุนั้นมีแค่ถูกเชื่อมโดยmorphismsหรือไม่ วัตถุทั้งหมดที่ถูกเชื่อมไปยังวัตถุที่ให้มาคือneighborของมัน ไม่เหมือนในชีวิตจริงที่ในcategory เพื่อนของเพื่อนของเพื่อนนั้นใกล้กว่าผมในฐานะเพื่อนสนิท ในcategoryที่ถูกเพิ่มค่าที่เหมาะสม เราสามารถที่จะนิยามระยะทางระหว่างวัตถุ

ได้มีอีกหนึ่งเหตุผลในทางปฏิบัติอย่างมากในการที่จะมีประสบการณ์ในการใช้งานcategoryที่ถูกเพิ่มค่าและนั้นก็เพราะว่า แหล่ข้องมูลที่มีประโยชน์อย่างมากเกี่ยวกับcategoryอย่างnLab ¹นั้นส่วนใหญ่ถูกเขียนในรูปแบบของcategoryที่ถูกเพิ่มค่า

29.1 ทำไมcategoryแบบmonoid?

ในการสร้างcategoryที่ถูกเพิ่มค่า เราต้องจำไว้ว่าเราควรที่จะนำนิยามทั่วๆไปกลับในตอนที่เราแทนที่categoryแบบmonoidด้วย$\textbf{Set}$และhom-objectsด้วยhom-sets วิธีการที่ดีืี่สุดในการทำแบบนี้คือการเริ่มด้วยนิยามทั่วๆไปและเปลี่ยนนิยามไปเรื่อยๆในแบบที่ไร้จุด นั้นก็คืนโดยที่ไม่มีีการเรียกสมาชิกของsetออกมา

เรามาเริ่มด้วยนิยามของการประกอบกัน โดนทั่วไปแล้วมันนำคู่ของmorphismsที่ตัวหนึ่งมาจาก$\textbf{C}(b,c)$และอีกตัวหนึ่งมาจาก$\textbf{C}(a,b)$ และโยงมันไปยังmorphismจาก$\textbf{C}(a, c)$ ในอีกความหมายหนึ่งมันคือการโยง

\[ \textbf{C}(b,c)\times\textbf{C}(a, b)\to\textbf{C}(a, c) \]

นี้คือfunctionระหว่างset ตัวหนึ่งของพวกมันเป็นproductแบบCartesianของสองhom-sets สูตรนี้นั้นสามารถถูดgeneralizeโดยการแทนที่productแบบCartesianด้วยบางอย่างที่กว้างกว่า productของcategoryอาจจะใช้ได้แต่เราสามารถไปไกลกว่านี้และใช้productแบบtensorแบบทั่วๆไปที่สุด

ต่อมาคือmorphisms identity แทนที่จะเลือกสมาชิกเดียวๆจากhom-sets เราสามารถนิยามพวกมันโดยการใช้functionจากsetที่มีสมาชิกเดียว$1$ว่า

\[ j_a::1\to\textbf{C}(a,a) \]

ในอีกครั้งสามารถแทนที่setที่มีสมาชิกเดียวด้วยวัตถุสุดท้ายแต่เราสามารถไปไกลกว่างโดนการแทนที่มันด้วยunit$i$ของproductแบบtensor

ในการที่คุณได้เห็น วัตถุที่นำมาจากบางcategoryแบบmonoid$\textbf{V}$นั้นคือตัวเลือกที่ดีสำหรับการแทนที่hom-set

29.2 categoryแบบmonoid

เราได้พูดไปแล้วสำหรับcategoryแบบmonoidก่อนหน้านี้ แต่มันคุ้มที่จะกล่าวถึงนิยามอีกครั้ง categoryแบบmonoidนิยามproductแบบtensorที่คือbifunctor

\[ \otimes :: \textbf{V}\times{}\textbf{V} \to \textbf{V} \]

เราต้องการproductแบบtensorที่มีคุณสมบัติการสลับหมู่แต่มันเพียงพอในการที่จะบรรลุความการสลับหมู่ จนไปถึงisomorphismธรรมชาติ isomorphismนี้นันถูกเรียกว่าassociator ส่วนประกอบมันคือ

\[ \alpha_{a b c} :: (a \otimes b) \otimes c \to a \otimes (b \otimes c) \]

มันต้องเป็นธรรมขาติในทั้งสามarguments

categoryแบบmonoidก็ต้องนิยามวัตถุunitพิเศษ$i$ที่ทำหน้าที่ในฐานะunitของproductแบบtensor ในอีกครั้งไปถึงisomorphismธรรมชาติ o isomorphismsทั้งสองถูกเรียกว่าunitorช้ายและขวาตามลำดับและส่วนประกอบของพวกมันคือ

\[ \begin{align*} \lambda_a & :: i \otimes a \to a \\ \rho_a & :: a \otimes i \to a \end{align*} \]

associatorและunitorsต้องบรรลุเงื่อนไขของความเข้ากันได้อย่าง

$\begin{tikzcd}[row sep=large] ((a \otimes b) \otimes c) \otimes d \arrow[d, "\alpha_{(a \otimes b)cd}"] \arrow[rr, "\alpha_{abc} \otimes \id_d"] & & (a \otimes (b \otimes c)) \otimes d \arrow[d, "\alpha_{a(b \otimes c)d}"] \\ (a \otimes b) \otimes (c \otimes d) \arrow[rd, "\alpha_{ab(c \otimes d)}"] & & a \otimes ((b \otimes c) \otimes d) \arrow[ld, "\id_a \otimes \alpha_{bcd}"] \\ & a \otimes (b \otimes (c \otimes d)) \end{tikzcd}$

$\begin{tikzcd}[row sep=large] (a \otimes i) \otimes b \arrow[dr, "\rho_{a} \otimes \id_b"'] \arrow[rr, "\alpha_{aib}"] & & a \otimes (i \otimes b) \arrow[dl, "\id_a \otimes \lambda_b"] \\ & a \otimes b \end{tikzcd}$

categoryแบบmonoidนั้นถูกเรียกว่าสมมาตรถ้าได้มีisomorphismธรรมชาติที่มีส่วนประกอบอย่าง

\[ \gamma_{a b} :: a \otimes b \to b \otimes a \]

ที่“กำลังสองแล้วเท่ากับหนึ่ง”

\[ \gamma_{b a} \circ \gamma_{a b} = \operatorname{id}_{a \otimes b} \]

และที่ตรงกันกับโครงสร้างmonoid

สิ่งที่น่าสนใจเกี่ยวกับcategoryแบบmonoidคือการที่ว่าคุณอาจจะสามารถที่จะนิยามhomภายใน(วัตถุfunctionในฐานะ)adjointด้านขวาของproductแบบtensor คุณอาจจะจำได้ว่านิยามดั้งเดิมของวัตถุfunctionหรือexponential นั้นผ่านadjointด้านขวาไปยังproductของcategory categoryที่วัตถุแบบนี้มีอยู่สำหรับคู่ของวัตถุใดๆก็ตามจะถูกเรีกยว่าCartesian closed ในที่นี้adjunctionที่นิยามhomภายในในcategoryแบบmonoidคือ

\[ \textbf{V}(a \otimes b, c) \sim \textbf{V}(a, [b, c]) \]

ตามาจากG. M. Kelly ² ผมได้ใช้เครื่องหมาย$[b,c]$สำหรับhomภายใน counitของadjunctionนี้คือการแปลงแบบธรรมชาติที่ส่วนประกอบถูกเรียกว่าmorphismsการประเมิน

\[ \varepsilon_{a b} :: ([a, b] \otimes a) \to b \]

สังเกตว่าถ้าproductแบบtensorนั้นไม่สมมาตร เราอาจจะนิยามhomภายในอีกตัวที่มีเครื่องหมาย$[[a,c]]$โดยการใช้adjunctionดังต่อไปนี้

\[ \textbf{V}(a \otimes b, c) \sim \textbf{V}(b, [[a, c]]) \]

categoryแบบmonoidที่ทั้งสองถูกนิยามว่าbiclosed ตัวอย่างของcategoryที่ไม่biclosedคือcategoryของendofunctorsใน$\textbf{Set}$ ที่การประกอบกันของfunctorนั้นมีหน้าที่ในฐานะproductแบบtensor นั้นคือcategoryที่เราใช้ในการนิยามmonadต่างๆ

29.3 Categoryที่ถูกเพิ่มค่า

category$\textbf{C}$ที่ถูกเพิ่มค่าบนcategoryแบบmonoid$\textbf{V}$แทนที่hom-setsด้วยhom-objects สำหรับทุกคู่ของวัตถุ$a$และ$b$ใน$\textbf{C}$ เราเชื่อมโยงวัตถุ$\textbf{C}(a,b)$ใน$\textbf{V}$ เราใช้เครื่องหมายสำหรับhom-objectsในตอนที่เราใช้สำหรับhom-sets กับความเข้าใจที่ว่าพวกมันไม่ได้มีmorphisms ในอีกด้านหนึ่ง$\textbf{V}$คือcategoryทั่วๆไป(ที่ไม่ได้ถูกเพิ่มค่า)กับhom-setsและmorphisms ดังนั้นเราไม่ได้ทิ้งsetทั้งหมด เราแค่ช่อนมันเอาไว้

เนื่องด้วยเราไม่สามารถพูดเกี่ยวกับmorphismsเดี่ยวๆใน$\textbf{C}$ การประกอบกันของmorphisms นั้นถูกแทนที่โดยชุดของmorphismsใน$\textbf{V}$

\[ \circ :: \textbf{C}(b, c) \otimes \textbf{C}(a, b) \to \textbf{C}(a, c) \]

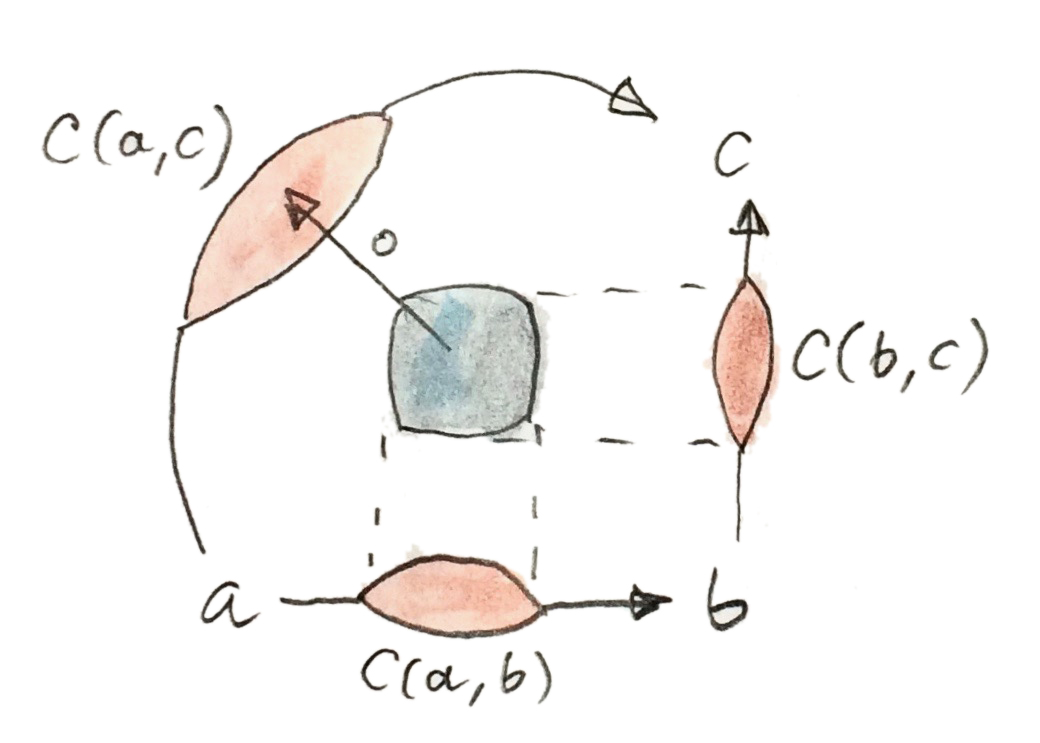
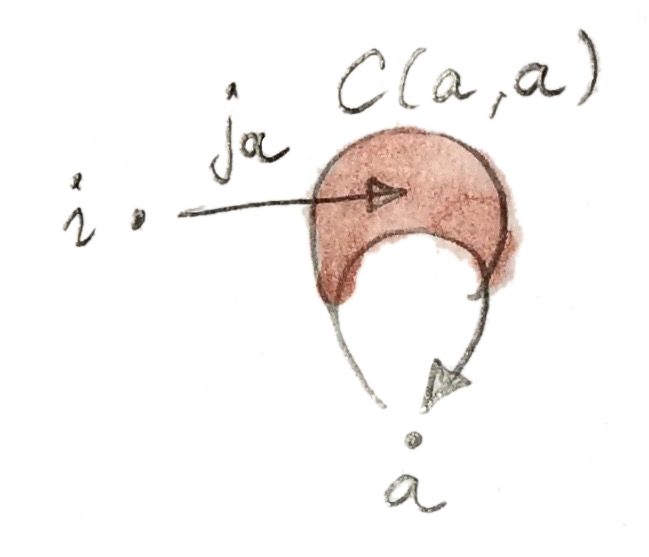
ในทางเดียวกัน morphisms identityนั้นถูกแทนที่โดยชุดของmorphismsใน$\textbf{V}$

\[ j_a :: i \to \textbf{C}(a, a) \]

ที่$i$นั้นคือunitของtensorใน$\textbf{V}$

ความสลับกลุ่มของการประกอบกันนั้นถูกนิยามในรูปแบบของassociatorใน$\textbf{V}$

$\begin{tikzcd}[column sep=large] (\textbf{C}(c,d) \otimes \textbf{C}(b,c)) \otimes \textbf{C}(a,b) \arrow[r, "\circ\otimes\operatorname{id}"] \arrow[dd, "\alpha"] & \textbf{C}(b,d) \otimes \textbf{C}(a,b) \arrow[dr, "\circ"] \\ & & \textbf{C}(a,d) \\ \textbf{C}(c,d) \otimes (\textbf{C}(b,c) \otimes \textbf{C}(a,b)) \arrow[r, "\operatorname{id}\otimes\circ"] & \textbf{C}(c,d) \otimes \textbf{C}(a,c) \arrow[ur, "\circ"] \end{tikzcd}$

กฏของunitในแบบเดียวกันถูกแสดงในรูปแบบของunitors

$\begin{tikzcd}[row sep=large] \textbf{C}(a,b) \otimes i \arrow[rr, "\operatorname{id} \otimes j_a"] \arrow[dr, "\rho"] & & \textbf{C}(a,b) \otimes \textbf{C}(a,a) \arrow[dl, "\circ"] \\ & \textbf{C}(a,b) \end{tikzcd}$

$\begin{tikzcd}[row sep=large] i \otimes \textbf{C}(a,b) \arrow[rr, "j_b \otimes \operatorname{id}"] \arrow[dr, "\lambda"] & & \textbf{C}(b,b) \otimes \textbf{C}(a,b) \arrow[dl, "\circ"] \\ & \textbf{C}(a,b) \end{tikzcd}$

29.4 Preorder

preorderนั้นถูกนิยามในฐานะcategoryที่บาง ที่ที่ทุกๆhom-setนั้นว่างหรือมีแค่สมาชิกเดียว เราตีความset$\textbf{C}(a,b)$ที่ไม่ว่างในฐานะข้อพิสูจน์ที่$a$นั้นน้อยกว่าหรือเท่ากับ$b$ categoryแบบนี้สามารถถูกตีความในฐานะที่ถูกเพิ่มค่าcategoryแบบmonoidที่เรียบง่ายอย่างมากที่เก็บแค่สองวัตถุ$0$และ$1$(ในบางครั้งถูกเรียกว่าเท็จและจริง) นอกเหนือmorphisms identityที่จำเป็น categoryนี้นั้นมีmorphismเพียงอันเดียวจาก$0$ไปยัง$1$ เรามาเรียกมันว่า$0\to1$ โครงสร้างmonoidแบบเรียบง่ายสามารถถูกสร้างจากมัน ด้วยproductแบบtensorออกแบบ การคำนวณของ$0$และ$1$(productที่ไม่ไช่ศูนย์เพียงอย่างเดียวคือ$1\otimes1$) วัตถุidentityในcategoryนี้คือ$1$ นี้คือcategoryแบบmonoidที่เคร่งก็เพราะว่าassociatorและunitorsคือmorphisms identity

เนื่องด้วยว่าในpreorder hom-setนั้นจะว่างหรือมีแค่สมาชิกเดียว เราสามารถแทนที่มันอย่างง่ายๆด้วยhom-objectสำหรับcategoryขนาดเล็กของเรา preorderที่ถูกเพิ่มค่า$\textbf{C}$มีhom-object$\textbf{C}(a,b)$สำหรับคู่ใดๆก็ตามของวัตถุ$a$และ$b$ ถ้า$a$นั้นน้อยกว่าหรือเท่ากับ$b$ วัตถุนี้คือ$1$ หรือไม่นั้นคือ$0$

เรามาดูที่การประกอบกัน productแบบtensorของสองวัตถุใดๆก็ตามคือ$0$เว้นแต่ว่าทั้งสองมันจะเป็น$1$ ที่ในกรณีนี้มันคือ$1$ ถ้ามันคือ$0$แล้วเรามีสองตัวเลือกสำหรับmorphismการประกอบ มันอยาจจะเป็นทั้ง$\operatorname{id}_0$หรือ$0\to1$ แต่ถ้ามันคือ$1$แล้วตัวเลือกเดี่ยวคือ$\operatorname{id}_1$ ถ้าเราทำการแปลงสิ่งนี้ให้กลับมายังความสัมพันธ์ สิ่งนี้บอกว่าถ้า$a\le b$และ$b\le c$แล้ว$a\le c$ที่คือกฏของการถ่ายทอดที่เราต้องการ

แล้วidentityละ? มันคือmorphismจาก$1$ไปยัง$\textbf{C}(a,a)$ ได้มีแค่morphismเดียวไปจาก$1$และนั้นคืิอidentity$\operatorname{id}_1$ ดังนั้น$\textbf{C}(a,a)$ต้องเป็น$1$ มันหมายความว่า$a\le a$ที่คือกฎของreflexivityสำหรับpreorder ดังนั้นทั้งการถ่ายทอดและreflexivity นั้นถูกบังคับใช้อย่างอัตโนมัติ ถ้าเราทำการเขียนpreorderในฐานะcategoryที่ถูกเพิ่มค่า

29.5 พื้นที่Metric

ตัวอย่างที่ที่น่าสนใจนั้นมาจาก William Lawvere ³ เขาสังเกตว่าพื้นที่Metricสามารถถูกนิยามโดยการใช้categoryที่ถูกเพิ่มค่า พื้นที่Metricนิยามระยะทางระหว่างสองวัตถุใดๆก็ตาม ระยะทางนี้คือจำนวนจริงที่ไม่ติดลบ มันนั้นสะดวกในการนำinfinityในฐานะค่าที่เป็นไปได้ ถ้าระยะนั้นคืิอinfinity ได้ไม่มีวิธีการในการไปจากจุดเริ่มต้นไปยังวัตถุเป้าหมาย

ได้มีบางคุณสมบัติที่ชัดเจนที่ต้องถูกบรรลุโดยระยะ หนึ่งในนั้นคือว่าระยะจากวัตถุไปยังตนเองต้องเป็นศูนย์ อีกตัวหนึ่งคืออสมการสามเหลี่ยมคือ ระยะโดยตรงนั้นไม่ใหญ่ไปกว่าผลบวกของระยะของจุดระหว่างกลาง เราไม่จำเป็นต้องให้ระยะทางนั้นสมมาตร ที่อาจจะดูแปลกในตอนแรกแต่ในการที่Lawvereอธิบาย คุณสามารถจินตนาการว่าในทิศหนึ่งคุณอาจจะเดินขึ้นเขา ในอีกทางหนึ่งคุณคุณอาจจะเดินลงเขา ในกรณีใดๆก็ตาม ความสมมาตรอาจจะถูกกำหนดหลังจากนี้ในฐานะเงื่อนไขเพื่มเติม

ดังนั้นวิธีการที่พื้นที่metricอาจจะถูกแปลงไปยังถาษาทางcategoryคืออะไร? เราต้องสร้างcategoryที่hom-objectsนั้นคือระยะ จงจำไว้ว่าระยะนั้นไม่ไช่morphismsแต่คือhom-object แล้วhom-objectจะเป็นตัวเลขได้อย่างไร? ถ้าเราสามารถสร้างcategoryแบบmonoid$\textbf{V}$ ที่เลขเหล่านี้นั้นคือวัตถุ จำนวนจริงที่ไม่ติดลบ (รวมไปถึงinfinity) ก่อให้เกิดorderแบบtotal ดังนั้นพวกมันสามารถถูกมองในฐานะcategoryบาง morphismหรัหว่างสองตัวเลข$x$และ$y$มีอยู่ถ้า$x\ge y$ (สิ่งนี้นั้นตรงกันข้ามกับสิ่งที่ใช้ในการนิยามของpreorder) โครงสร้างmonoidนั้นให้มาโดยการบวก ที่เลขศูนย์นั้นมีหน้าที่เป็นวัตถุunit ในอีกความหมายหนึ่งproductแบบtensorของสองตัวเลขคือผลบวกของมัน

พื้นที่metricนั้นคือcategoryที่ถูกเพิ่มค่าบนcategoryแบบmonoidal hom-object$\textbf{C}(a,b)$จากวัตถุ$a$ไปยัง$b$นั้นไม่ได้ติดลบ (และอาจจะinfinite) ตัวเลขที่เราจะเรียกระยะจาก$a$ไปยัง$b$ เรามาดูกันว่าสิ่งที่เราได้มาสำหรับidentityและการประกอบกันในcategoryแบบนั้น

โดยนิยามของเรา morphismจากunitแบบtensorที่คือคัวเลขศูนย์ไปยังhom-object$\textbf{C}(a,a)$ คือความสัมพันธ์

\[ 0\le\textbf{C}(a,a) \]

เนื่องด้วย$\textbf{C}(a,a)$คือตัวเลขมี่ไม่ติดลบ เงื่อนไขนี้บอกเราว่าระยะจาก$a$ไปยัง$a$นั้นต้องเป็นศูนย์ ลองตรวจสอบ!

ในตอนนี้เรามาพูดเกี่ยวกับการประกอบกัน เราเริ่มด้วยproductแบบtensorของhom-objectsที่ติดกันของ$\textbf{C}(b,c)\otimes\textbf{C}(a,b)$ เราได้นิยามproductแบบtensorในฐานะการบวกของสองระยะ การประกอบกันคือmorphismใน$\textbf{V}$จากproductนี้ไปยัง$\textbf{C}(a,c)$ morphismใน$\textbf{V}$นั้นถูกนิยามในฐานะความสัมพันธ์ที่มากกว่าหรือเท่ากับ ในอีกความหมายหนึ่ง ผลบวกของระยะจาก$a$ไปยัง$b$ และจาก$b$ไปยัง$c$นั้นมากกว่าหรือเท่ากับระยะจาก$a$ไปยัง$c$ แต่นั้นแต่นั้นคือแค่อสมการสามเหลี่ยม ลองตรวจสอบ!

ในการแปลงพื้นที่metricใหม่ในรูปแบบของcategoryที่ถูกเพิ่มค่า เราได้อสมการสามเหลี่ยมและระยะกับตัวเองที่เป็นศูนย์“โดยไม่มีอะไร”

29.6 Functorsที่ถูกเพิ่มค่า

นิยามของfunctorนั้นเกี่ยวข้องกับกับการโยงของmorphismต่างๆ ในลักษณะของการถูกเพิ่มค่านี้ เราไม่ต้องมีแนวคิดของmorphismsเดี่ยวๆ ดังนั้นเราต้องทำงานกับhom-objectเป็นกลุ่ม hom-objectคือวัตถุในcategoryแบบmonoid$\textbf{V}$ และเรามีmorphismระหว่างพวกมันให้ได้ใช้ ดังนั้นมันมีเหตุผลในการนิยามfunctorsที่ถูกเพิ่มค่าระหว่างcategoryในตอนที่พวกมันถูกเพิ่มค่าบนcategoryแบบmonoid$\textbf{V}$ ดังนั้นเราได้ใช้morphismsใน$\textbf{V}$ของการโยงhom-objectsระหว่างcategoriesที่ถูกเพิ่มค่าสองตัว

Functorsที่ถูกเพิ่มค่า$F$ระหว่างสองcategories$\textbf{C}$และ$\textbf{D}$นอกเหนือจากการโยงวัตถุไปยังวัตถุ นั้นก็กำหนดไปยังทุกๆคู่ของวัตถุใน$\textbf{C}$ morphismใน$\textbf{V}$

\[ F_{a b} :: \textbf{C}(a, b) \to \textbf{D}(F\ a, F\ b) \]

functorนั้นคือการโยงที่คงไว้ในโครงสร้าง สำหรับfunctorsทั่วๆไปมันหมายถึงการคงไว้ซึ่งการประกอบกันและidentity ในลักษณะของการถูกเพิ่มค่านี้ การคงไว้ซึ่งการประกอบกันหมายความว่าdiagramดังต่อไปนี้commute

$\begin{tikzcd}[column sep=large, row sep=large] \textbf{C}(b,c) \otimes \textbf{C}(a,b) \arrow[r, "\circ"] \arrow[d, "F_{bc} \otimes F_{ab}"] & \textbf{C}(a,c) \arrow[d, "F_{ac}"] \\ \textbf{D}(F\ b, F\ c) \otimes \textbf{D}(F\ a, F\ b) \arrow[r, "\circ"] & \textbf{D}(F\ a, F\ c) \end{tikzcd}$

การคงอยู่ของidentityนั้นแทนที่โดยการคงอยู่ของmorphismsใน$\textbf{V}$ที่“เลือก”identity

$\begin{tikzcd}[row sep=large] & i \arrow[dl, "j_a"'] \arrow[dr, "j_{F a}"] & \\ \textbf{C}(a,a) \arrow[rr, "F_{aa}"] & & \textbf{D}(F\ a, F\ a) \end{tikzcd}$

29.7 การเพิ่มค่าตนเอง(Self Enrichment)

categoryแบบmonoidที่ปิดและสมมาตรอาจจะเป็นตัวที่เพิ่มค่าตนเองโดยการแทนที่hom-setsด้วยhomsภายใน (ลองดูนิยามข้างบน) ในการทำให้สิ่งนี้ใช้ได้ เราต้องนิยามกฏของการประกอบสำหรับhomsภายใน ในอีกความหมายหนึ่ง เราต้องเขียนmorphismกับsignatureดั่งต่อไปนี้

\[ [b, c] \otimes [a, b] \to [a, c] \]

สิ่งนี้นั้นไม่ต่างกันมากจากงานการเขียนโปรแกรมอื่นๆต่างกันแค่ว่าในทฤษฎีcategory เรามักจะให้การเขียนแบบไม่มีจุด เราเริ่มโดยการกำหนดsetที่สมาชิกที่ควรจะเป็นของมัน ในกรณีนี้มันคือสมาชิกของhom-set

\[ \textbf{V}([b, c] \otimes [a, b], [a, c]) \]

hom-setนี้นั้นisomorphicกับ

\[ \[\textbf{V}(([b, c] \otimes [a, b]) \otimes a, c)\] \]

ผมได้ใช้แค่adjunctionที่นิยามhomภายใน$[a,c]$ ถ้าเราสร้างmorphismในsetใหม่นี้ adjunctionจะชี้เราไปยังmorphismในsetดั้งเดิมที่เราก็สามารถใช้ในฐานะการประกอบกัน เราสร้างmorphismนี้โดยการประกอบmorphismsหลายๆตัวที่เรามีพร้อมไว้อยู่ เราเริ่มด้วยการที่เราสามารถใช้associator$\alpha_{[b,c],[a,b],a}$ในการสลับกลุ่มของสูตรทางด้านช้าย

\[ [([b, c] \otimes [a, b]) \otimes a \to [b, c] \otimes ([a, b] \otimes a) \]

เราก็ตามมันด้วยcounitของadjunction$\varepsilon_{a b}$:

\[ [b, c] \otimes ([a, b] \otimes a) \to [b, c] \otimes b \]

และใช้counit$\varepsilon_{b c}$อีกครั้งในการได้มาซึ่ง$c$ ดังนั้นเราได้สร้างmorphismของ

\[ \varepsilon_{b c}\ .\ (\operatorname_{[b, c]} \otimes \varepsilon_{a b})\ .\ \alpha_{[b, c] [a, b] a} \]

ที่คือสมาชิกของhom-set

\[ \[\textbf{V}(([b, c] \otimes [a, b]) \otimes a, c)\] \]

adjunctionนี้จะให้เราได้กฎของประกอบที่เรากำลังตามหา

ในแบบเดียวกันidentityคือ

\[ j_a :: i \to [a, a] \]

คือสมาชิกของhom-setดั่งต่อไปนี้

\[ \textbf{V}(i, [a, a]) \]

ที่isomorphicผ่านadjunctionอย่าง

\[ \[\textbf{V}(i \otimes a, a)\] \]

เรารู้ว่าhom-setนี้มีidentityด้านช้าย$\lambda_a$ เราสามารถนิยาม$j_a$ในฐานะimageของมันภายใต้adjunctionนี้

ตัวอย่างที่ใช้ได้จริงของการเพิ่มค่าตนเองคือcategory$\textbf{Set}$ที่ทำหน้าที่ในฐานะต้นแบบของtypesในภาษาโปรแกรม เราได้เห็นก่อนหน้านี้ว่ามะนคือcategoryแบบmonoidปิดคู่กับproductของCartesian ใน$\textbf{Set}$ hom-setระหว่างสองsetใดๆก็ตามคือsetเอง ดังนั้นมันคือวัตถุใน$\textbf{Set}$ เรารู้ว่ามันisomorphicกับsetของexponential ดังนั้นhomsภายนอกและภายในจรึงเท่าเทียมกัน ดังนั้นในตอนนี้เราก็รู้ว่า ผ่านการเพิ่มค่าตนเอง เราสามารถใช้setของexponentialในฐานะhom-objectและแสดงการประกอบกันในรูปแบบของproductsแบบCartesianของวัตถุexponential

29.8 ความสัมพันธ์กับ2-Categories

ผมได้พูดเกี่ยวกับ$\textbf{2}$-categoryในบริบทของ$\textbf{Cat}$ categoryของcategoryขนาดเล็ก morphismsระหว่างcategoryนั้นคือfunctors แต่ก็ได้มีโครงสร้างเพิ่มเติมคือการแปลงแบบธรรมชาติระหหว่างfunctors ใน$\textbf{2}$-category วัตถุมันจะถูกเรียกว่าzero-cell morphismsคือ1-cell และmorphismsระหว่างmorphismsคือ2-cells ใน$\textbf{Cat}$ 0-cellsคือcategory 1-cellsคือfunctorsและ2-cellsคือการแปลงแบบธรรมชาติ

แต่สังเกตว่าfunctorsระหว่างสองcategoryก่อให้เกิดcategoryเช่นเดียวกัน ดังนั้นใน$\textbf{Cat}$ เราจำเป็นต้องมีhom-categoryแทนที่จะเป็นhom-set มันกลับกลายเป็นว่า เหมือนกับ$\textbf{Set}$ที่สามารถถูกมองในฐานะcategoryที่ถูกเพ่ิมค่าบน$\textbf{Set}$ $\textbf{Cat}$สามารถที่จะถูกมองในฐานะcategoryที่ถูกเพ่ิมค่าบน$\textbf{Cat}$ ให้กว้างไปกว่านั้น แค่เหมือนกับทุกๆcategoryสามารถถูกมองในฐานะcategoryที่ถูกเพ่ิมค่าบน$\textbf{Set}$ ทุกๆ$\textbf{2}$-categoryสามารถถูกมองในการเพ่ิมค่าบน$\textbf{Cat}$