12 การเขียนโปรแกรมแบบdeclarative(ประกาศ) (Sketch)
ในส่วนแรกของหนังสือเล่มนี้ผมได้เสนอว่าทั้งทฤษฎีcategoryและการเขียนโปรแกรมนั้นเกี่ยวกับการประกอบกัน ในการเขียนโปรแกรมคุณทำการแยกปัญหาไปเรื่อยๆจนอยู่ในระดับของรายระเอียดที่คุณสามารถทำงานกับมันได้ และทำการแก้ปัญหาย่อยๆในแต่ละตัวและประกอบคำตอบใหม่จากล่างขึ้นบน ถ้าให้พูดแบบคร่าวๆได้มีสองวิธีในการทำแบบนี้คือการบอกคอมพิวเตอร์ในสิ่งที่ต้องทำ หรือบอกวิธีการทำให้มัน วิธีหนึ่งเรียกว่าdeclarativeและอีกอันหนึ่งคือimperative
คุณสามารถเห็นสิ่งนี้แม้ในระดับที่พื้นฐานที่สุด การประกอบกันเองอาจจะถูกนิยามในแบบdeclarative เหมือนในhคือการประกอบของgที่ตามมาจากf
h = g . fหรือในแบบของimperativeเหมือนในการเรียกfก่อน จำผลของการเรียกนี้แล้วก็เรียกgกับผลลัพธ์
h x = let y = f x
in g yในแบบของการโปรแกรมแบบimperativeนั้นมักจะถูกอธิบายในฐานะการกระทำต่อเนื่องที่ลำดับในเวลา โดยเฉพาะในการเรียกgไม่สามารถเป็นไปได้ก่อนการใช้งานfจะเสร็จก่อน อย่างน้อยนั่นคือภาพของแนวคิดในภาษาที่ขี้เกียจ(lazy)ที่มีการเรียกแบบเท่าที่ต้องการ(call-by-need) ของการนำargumentมา การใช้งานจริงๆแล้วอาจจะดำเนินการในแบบที่แตกต่าง
ในความเป็นจริงถ้าขึ้นอยู่กับความฉลาดของcomplierแล้ว มันไม่ค่อยมีความแตกต่างหรือแทบไม่มีระหว่างวิธีการที่โค้ดแบบdeclarativeและimperativeจะถูกประมวล แต่ทั้งสองวิธีการนั้นมีความแตกต่างอย่างมาก ในวิธีการที่เราจะเข้าหาการแก้ปัญหา และในความสามารถในการดูแลและทดสอบของโค้ดที่ถูกเขียน
คำถามหลักคือในตอนที่เราเผชิญหน้ากับปัญหา เราจะมีทางเลือกระหว่างแนวทางของdeclarativeและimperativeในการแก้ปัญหา ตลอดหรือเปล่า? และถ้าได้มีคำตอบแบบdeclarativeแล้วมันสามารถถูกแปลไปยังโค้ดของคอมพิวเตอร์ได้หรือเปล่า? คำตอบของคำถามนี้นั้นไม่ตรงไปตรงมาและถ้าเราอาจตอบมันได้ เราอาจจะปฏิวัติความเข้าใจของเราของจักรวาล
ให้ผมได้อธิบายเพิ่ม ได้มีdualityคล้ายๆกันในฟิสิกส์ที่ทั้งชี้ไปยังบางหลักการที่ลึกชึ้งภายใต้ หรือบอกเราบางอย่างเกี่ยวกับวิธีการที่จิตใจทำงาน Richard Feynmanได้เอ่ยถึงถึงdualityนี้ ที่เป็นแรงบันดาลใจของผลงานของเขาที่เกี่ยวกับ quantum electrodynamics
ได้มีสองรูปแบบของการแสดงกฏส่วนใหญ่ของฟิสิกส์อกกมา หนึ่งในนั้นคือการใช้การพิจารณาเฉพาะแห่ง(local)หรือที่มีขนาดเล็กอย่างมาก(infinitesimal) เรามองไปที่สภาพของระบบในบริเวณข้างเคียง(neighborhood)รอบๆและทำการคาดเดาการที่มันเปลี่ยนแปลงภายในเวลาถัดไปอันสั้น สิ่งนี้มักจะถูกแสดงโดนการใช้สมการdifferentialที่ต้องถูกintegratedหรือบวกรวมกันในช่วงๆหนึ่งของเวลา
สังเกตวิธีนี้นั้นมีความคล้ายกับการคิกแบบimperativeคือการที่เราไปยังคำตอบสุดท้าย โดยการตามเป็นลำดับของขั้นเล็กๆที่แต่ละตัวที่ขึ้นอยู่กับผลลัพธ์ของลำดับก่อนหน้า ในความเป็นจริงแล้วการsimulationโดยคอมพิวเตอร์ของระบบทางฟิสิกส์นั้นมักจะถูกเขียน โดยการแปลงสมการdifferentialไปยังสมการdifferenceและทำการทำซ้ำมัน นี่คือวิธีการที่ยานอวกาศถูกทำให้เคลื่อนไหวได้ในเกมasteroids ในแต่ละขั้นของเวลา ตำแหน่งของยานอวกาศนันถูกเปลี่ยนโดยการบวกเพิ่มขึ้นอย่างเล็กน้อย ที่ถูกคำนวนโดยการคูณความเร็วของมันกับเวลาdelta ส่วนความเร็วนี้นก็ถูกเปลี่ยนโดยการบวกเพิ่มขึ้นอย่างเล็กน้อยในสัดส่วนของความเร่งที่ถูกให้มาโดยแรงหารด้วยมวล
ได้มีการเขียนโดยตรงของสมการdiffferentialที่ตรงกันกับกฎการเคลื่อนที่ของNewton
\[ \begin{align*} F & = m \frac{dv}{dt} \\ v & = \frac{dx}{dt} \end{align*} \]
ได้มีวิธีการคล้ายๆกันสามารถถูกใช้ในปัญหาที่ชับช้อนต่างๆอย่างการแพร่ขยายอย่างของสนามแม่เหล็กไฟฟ้า โดยการใช้สมการของMaxwellหรือแม้กระทั่งพฤติกรรมของquarksและgluonsภายในprotonโดยการใช้QCD (quantum chromodynamics)แบบlattice
การคิดแบบเฉพาะแห่งแบบนี้ถูกรวบกับการdiscretization(ทำให้เป็นช่วงๆ)ของพื้นที่และเวลา ที่ถูกสนับสนุนโดยการใช้คอมพิวเตอร์แบบดิจิตอล ได้แสดงออกมาอย่างสุดโต่งในความพยายามที่กล้าหาญของStephen Wolfram ในการลดความชับช้อนของจักรวาลทั้งหมดไปยังระบบของ cellular automata
ในอีกวิธีหนึ่งนั้นคือแบบสากล(global) เรามองไปที่สภาพเริ่มตันและสภาพสุดท้ายของระบบและคำนวนเส้นทางที่เชื่อมพวกมันโดยการลดขนาด ของบางfunctional ตัวอย่างที่ง่ายที่สุดคือหลักการของเวลาที่น้อยที่สุดของFermat มันบอกว่าลำแสงที่แพร่ตามเส้นทางที่ใช้เวลาในการเดินทางที่น้อยที่สุด โดยเฉพาะในการไม่มีวัตถุที่สะท้อนหรือหักเห ลำแสงจากจุด\(A\)ไปยัง\(B\)จะใช้เส้นทางที่สั้นที่สุดที่ก็คือเส้นตรง แต่แสงจะเคลื่อนที่ในเวลาที่ช้าลงในวัสดุที่มีความหนาแน่น(และโปร่งแสง)อย่างน้ำหรือแก้ว ดังนั้นถ้าคุณเลือกจุดเริ่มต้นในอากาศและในจุดสุดท้ายภายใต้น้ำ มันนั้นมีประโยชน์มากกว่าสำหรับแสงที่จะเดินทางได้นานกว่าในอากาศและก็ใช้ทางลัดผ่านน้ำ เส้นทางของเวลาที่น้อยที่สุดทำให้ลำแสงหักเหที่ขอบระหว่างอากาศและน้ำ โดยผลที่ตามมาคือกฏการหักเหของSnell
\[ \frac{\sin(\theta_1)}{\sin(\theta_2)} = \frac{v_1}{v_2} \]
ที่ที่\(v_1\)คือความเร็วของแสงในอากาศและ\(v_2\)คือความเร็วของแสงในน้ำ

กลศาสตร์ดั้งเดิมทั้งหมดสามารถเกิดมาจากหลักการการกระทำที่น้อยที่สุด(principle of least action) การกระทำสามารถถูกคำนวนสำหรับเส้นทางใดๆก็ตามโดยการintegrate Lagrangianที่ก็คือความแตกต่างระหว่างพลังงานจลน์และพลังงานศักย์ (สังเกตว่า มันคือความแตกต่างไม่ใช่การบวกกัน การบวกกันหมายถึงพลังงานทั้งหมด) ในตอนที่คุณยิงปืนครกเพื่อที่จะชนเป้าหมายที่ให้มา กระสุนยิงนั้นจะเคลื่อนขึ้นข้างบนก่อนที่พลังงานศักย์ที่มาจากแรงโน้มถ่วงนั้นมีมากกว่า และจะใช้บางเวลาตรงนั้นในการรวบรวมด้านที่เป็นลบในการกระทำ แล้วมันจะเร่งความเร็วเพื่อที่จะเคลื่อนที่อย่างรวดเร็วผ่านพื้นที่ที่มีพลังงานศักย์น้อย
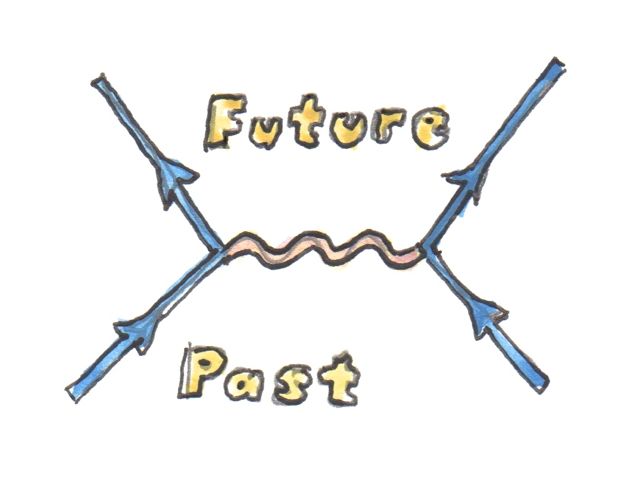
ผลงานของFeynmanที่ยิ่งใหญ่ที่สุดคือการนึงถึงได้ว่าหลักการการกระทำที่น้อยสามารถถูกใช้(generalized) ไปยังกลศาสตร์ควอนตัม ในอีกครั้งที่ปัญหาคือการแสดงออกในรูปสูตรของสภาพเริ่มต้นและสภาพสุดท้าย path integralของFeynmanระหว่างสภาพเหล่านี้ถูกใช้ในการคำนวนความเป็นไปได้ของการเปลี่ยนแปลง
ประเด็นอยู่ที่ว่าได้มีdualityที่ไม่ได้ถูกอธิบายและน่าสนใจในการที่เราสามารถอธิบายกฏของphysics เราสามารถใช้ภาพแบบเฉพาะแห่งที่สิ่งต่างๆเกิดขึ้นเเป็นลำดับและในการเพื่มขึ้นอย่างเล็กๆ หรือเราสามารถใช้ภาพแบบสากลที่ที่เราประกาศเงื่อนไขเริ่มและเงื่อนไขสุดท้ายและทุกๆอย่างระหว่างมันก็จะตามมา
ในวิธีทางแบบสากลก็สามารถถูกใช้ในการเขียนโปรแกรมตัวอย่างเช่นในการเขียนray tracing เราประกาศตำแหน่งของตาและตำแหน่งของแหล่งของแสง และหาเส้นทางที่ลำแสงอาจจะเชื่อมพวกมันเข้าด้วยกัน เราไม่ได้ลดเวลาในการเคลื่อนที่อยากเปิดเผยของแต่ละลำแสง แต่เราใช้กฏของSnellและเรขาคณิตของการสะท้อนที่ที่ได้ผลเหมือนกัน
ความแตกต่างที่ใหญ่ที่สุดระหว่างวิธีแบบเฉพาะแห่งและแบบสากลคือการที่พวกมันพิจารณาพื้นที่และสำคัญไปกว่านั้นคือเวลา วิธีแบบเฉพาะแห่งยอมรับความพึงพอใจแบบฉับพลันของที่นี้และตรงนี้ ในขณะที่วิธีแบบสากลนั้น มีมุมมองที่อยู่กับที่ในระยะยาว อย่างกับว่าอนาคตได้ถูกกำหนดไว้แล้ว และเราแค่วิเคราะห์คุณสมบัติของจักรวาลนิรันดร
ไม่มีที่ไหนที่สามารถจะแสดงให้เห็นได้ดีไปกว่าแนวทางของFunctional Reactive Programming (FRP)กับการปฏิสัมพันธ์ของผู้ใช้ โดยแทนที่จะเขียนhandlersแยกกันสำหรับการกระทำของผู้ใช้ในทุกๆรูปแบบ ทั้งหมดมีการเข้าถึงต่อstateที่เป็นส่วนรวมและสามารถเปลี่ยนได้ FRPพิจารณาเหตุการภายนอกในฐานะรายการที่ไม่มีที่สิ้นสุดและใช้การเปลี่ยนแปลงหลายๆอย่างกับมัน ในทางแนวคิดแล้ว รายการของการกระทำของเรานั้นอยู่ที่นี่และมีอยู่แล้วในฐานะข้องมูลinputกับโปรแกรมของเรา ในมุมมองของโปรแกรม ไม่มีความแตกต่างระหว่างlistของตัวเลขของ\(\pi\) listของเลขสุ่มเทียมหรือlistของตำแหน่งmouseที่มาจากhardwareของคอมพิวเตอร์ ในแต่ละกรณีถ้าคุณต้องไปยังตัวเลขในตำแหน่งที่\(n\)th คุณต้องผ่านทั้ง\(n-1\)ตัวเลขก่อน ในตอนใช้กับเหตุการที่ขึ้นกับเวลา เราเรียกคุณสมบัตินี้ว่าcausality(ความสัมพันธ์ระหว่างเหตุและผล)
แล้วสิ่งนี้เกี่ยวกับทฤษฎีcategoryอย่างไร? ผมจะเสนอว่าทฤษฎีcategoryนั้นสนับสนุนแนวทางแบบสากลและดังนั้นรองรับการเขียนโปรแกรมแบบdeclarative ก่อนอื่นเลยคือไม่เหมือนcalculus มันไม่มีเครื่องหมายที่มีอยู่แล้วของระยะทางหรือบริเวณข้างเคียงหรือเวลา สิ่งที่เรามีอยู่ทั้งหมดคือวัตถุนามธรรมและการเชื่อมต่อที่เป็นนามธรรมระหว่างมัน ถ้าคุณสามารถไปจาก\(A\)ไปยัง\(B\)ผ่านลำดับของขั้นต่างๆ คุณสามารถที่จะไปได้ในกระโดดครั้งเดียว มากไปกว่านั้น เครื่องมือส่วนใหญ่ทฤษฎีcategoryคือการสร้างแบบสากลที่เป็นจุดสูงสุดของแนวทางแบบสากล เราได้เห็นมันในการใช้งานแล้ว ตัวอย่างเช่นในนิยามของproductแบบcategorical มันสามารถถูกทำได้โดยการกำหนดคุณสมบัติของมัน (ที่เป็นแนวทางที่declarativeอย่างมาก มันคือวัตถุที่ที่projectionสองตัวและเป็นวัตถุที่ดีที่สุด) มันทำให้บางคุณสมบัติมีประโยชน์ที่สุด ที่ก็คือคุณสมบัติของการแยกตัวประกอบของprojectionของวัตถุอื่นๆ
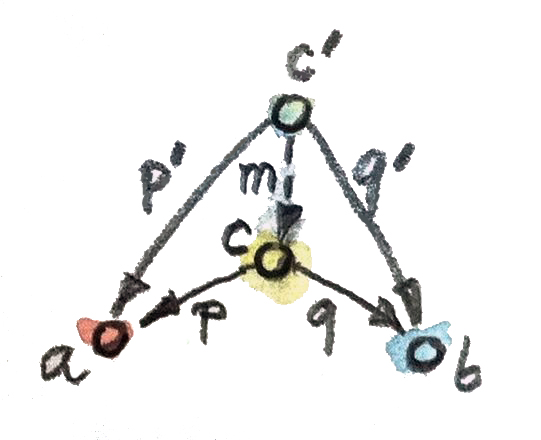
เทียบกับหลักการของเวลาที่น้อยที่สุดของFermatหรือหลักการการกระทำที่น้อยที่สุด
ในทางกลับกัน แตกต่างกับนิยามที่มีมาก่อนของproductแบบCartesianที่มีความimperativeมากกว่า คุณนิยามวิธีการสร้างสมาชิกของproductโดยการเลือกหนึ่งสมาชิกของsetหนึ่งและสมาชิกอีกตัวจากอีกsetหนึ่ง มันคือสูตรในการสร้างpairและนั้นคืออีกวิธีหนึ่งในการแยกส่วนของpair
ในแทบทุกๆภาษาโปรแกรมรวมไปถึงภาษาfunctionalเหมือนHaskellอย่าง typeแบบproduct coproduct function นั้นถูกสร้างอยู่แล้ว แทนที่จะถูกนิยามโดยการสร้างแบบสากล ถึงแม้ได้มีความพยายามในการสร้างภาษาโปรแกรมแบบcategory (อย่างวิทยานิพนธ์ของTatsuya Hagino1)
ไม่ว่าจะใช้มันโดยตรงหรือไม่ นิยามแบบcategoryพิสูจน์ว่าการสร้างแบบการเขียนโปรแกรมที่มีอยู่แล้วนั้นถูกต้องแลัวก็ทำให้เกิดการสร้างใหม่ๆ สำคัญไปกว่านี้คือทฤษฎีcategoryให้ ภาษาของภาษา(meta-language)สำหรับการให้เหตุผลเกี่ยวกับโปรแกรมคอมพิวเตอร์ในระดับของการประกาศ มันก็สนับสนุนการให้เหตุผลเกี่ยวกับกฏเกณฑ์ของปัญหาก่อนที่มันจะถูกเขียนไปในโค้ด