18  มันเกี่ยวกับmorphismทั้งหมด (Sketch)

ถ้าผมไม่ได้ทำให้คุณมั่นใจว่าทฤษฎีcategoryนั้นเกี่ยวกับmorphismทั้งหมดแล้วผมก็ยังไม่ได้ทำงานของผมอย่างถูกต้อง เนื่องด้วยหัวข้อต่อไปคือadjunctionที่ถูกนิยามในแบบของisomorphismของhom-set มันมีเหตุมีผลในการทบทวนความเข้าใจของเราเกี่ยวกับส่วนก่อสร้างของhom-set แล้วก็คุณจะเห็นว่าadjunctionให้มากกว่าภาษาทั่วไปในการบรรยายการสร้างหลายๆแบบที่เราได้ศึกษามาก่อนหน้านี้ ดังนั้นมันอาจจะช่วยในการทบทวนพวกมันด้วย

18.1 Functors

เริ่มต้นคุณควรที่จะคิดถึงfunctorในฐานะการโยงของmorphism (มุมมองที่เน้นย้ำในนิยามในHaskellของtypeclassFunctorที่หมุนรอบfmap) แน่นอนว่าfunctorสามารถโยงวัตถุ(จุดปลายของmorphism)อีกอย่างหนึ่งเราอาจจะไม่สามารถในการพูดถึงการคงไว้ในการประกอบ วัตถุบอกเราว่าคู่ตัวใหนของmorphismนั้นสามารถประกอบได้ เป้าของmorphismนึ่งต้องเท่ากับจุดเริ่มต้นของอีกตัวหนึ่ง ถ้าพวกมันจะถูกประกอบ ดังนั้นถ้าเราต้องการประกอบกันของmorphismในการโดนถูกโยงไปยังการประกอบกันของmorphismที่ถูกlift การโยงของจุดปลายของพวกมันนั้นก็แทบจะถูกกำหนดแล้ว

18.2 DiagramของการCommute

คุณสมบัติหลากหลายต่างของmorphismถูกแสดงในรูปของdiagramของการcommute ถ้าบางmorphismสามารถถูกอธิบายในฐานะการประกอบกันของmorphsimอีกกันในวิธีการมากกว่าหนึ่งแล้วเราจะมีdiagramของการcommute

โดยเฉพาะ diagramของการcommuteก่อให้เกิดพื้นฐานของแทบทุกๆการสร้างแบบสากล (ที่มีข้อยกเว้นที่น่าสนใจอย่างวัตถุเรื่มต้นและวัตถุสุดท้าย) เราได้เห็นแล้วว่าในนิยามของproduct coproductและ(co-)limitมากมาย วัตถุexponential monoidแบบfree และอื่นๆ

productนี้คือตัวอย่างที่เรียบง่ายของการสร้างแบบสากล เราเลือกสองวัตถุ\(a\)และ\(b\)และเห็นถ้าได้มีวัตถุ\(c\)รวมกันกับคู่ของmorphism\(p\)และ\(q\)ที่มีคุณสมบัติสากลชองการเป็นproductของพวกมัน

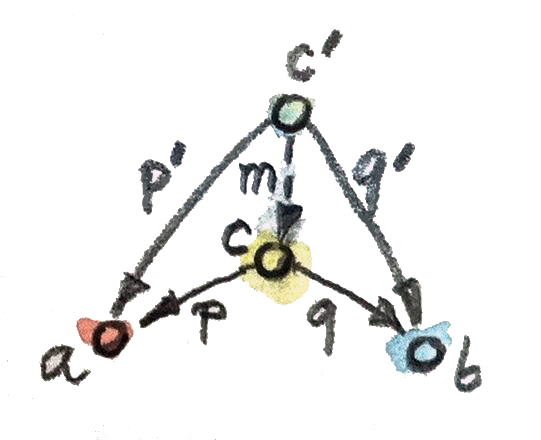
productคือกรณีพิเศษของlimit limitถูกนิยามในรูปแบบของcones coneแบบทั่วไปถูกสร้างจากdiagramของการcommute ความcommutativeของdiagramเหล่านี้อาจจะถูกแทนที่ด้วยเงื่อนไขความเป็นธรรมชาติสำหรับการโยงของfunctor ความcommutativeแบบนี้ถูกลดไปเป็นบทบาทของภาษาassemblyสำหรับภาษาที่อยู่ขั้นสูกกว่าของการแปลงแบบธรรมชาติ

18.3 การแปลงแบบธรรมชาติ

โดยทั่วไปแล้วการแปลงแบบธรรมชาตินั้นสะดวกอย่างมากในตอนที่เราต้องการที่จะโยงจากmorphismไปยังสี่เหลี่ยมของการcommute ด้านตรงข้ามทั้งสองของสี่เหลี่ยมของการcommuteคือการโยงของบางmorphism\(f\)ภายใต้สองfunctorอย่าง\(F\)และ\(G\) ในอีกด้านหนึ่งคือส่วนประกอบของการแปลงแบบธรรมชาติ (ที่ก็คือmorphism)

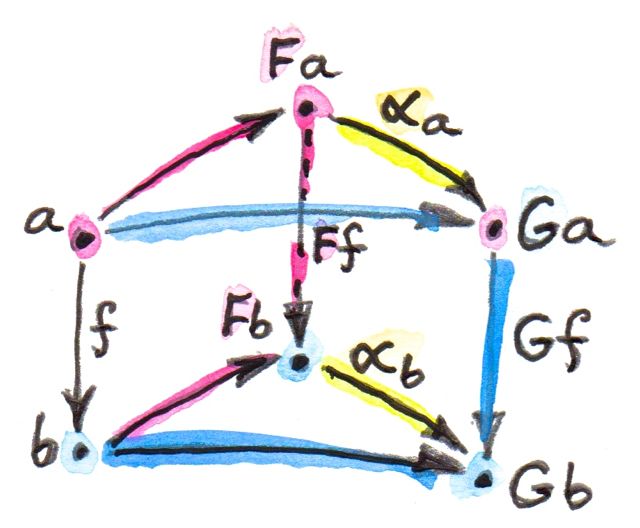
ความเป็นธรรมชาติหมายความว่าในตอนที่คุณเคลื่อนที่ไปยังส่วนประกอบ”รอบๆ”(โดยสิ่งรอบๆผมหมายความว่าถูกเชื่อมโดยmorphism)คุณไม่ได้ทำสวนกับโครงสร้างของทั้งcategoryหรือfunctor มันไม่สำคัญ ถ้าคุณใช้ส่วนประกอบของของการแปลงแบบธรรมชาติก่อนในการเชื่อมข้่องว่าระหว่างวัตถุแล้วก็กระโดดไปยังส่วนรอบๆของมันโดนการใช้functorหรือในอีกทางหนึ่ง ทิศทางทั้งสองนั้นตั้งฉากกัน การแปลงแบบธรรมชาติเคลื่อนด้านช้ายของคุณไปยังด้านขวาและfunctorเคลื่อนคุณไปด้านบนและล่างหรือข้านหน้าและกลับหลัง จะว่าไปแล้ว คุณสามารถที่จะนึกภาพimageของfunctorในฐานะแผ่นในcategoryป้าหมาย การแปลงแบบธรรมชาติโยงแผ่นแบบนี้ที่คู่กับ\(F\)ไปยังอีกอันหนึ่งที่คู่กับ\(G\)

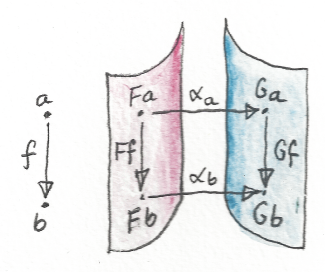
เราได้เห็นตัวอย่างของความตั้งฉากกันในHaskell นัน้คือการกระทำของfunctorที่แก้ไขสิ่งที่อยู่ในภาชนะโดยที่ไม่ต้องเปลี่ยนรูปทรงของมัน ในขณะเดียวกันการแปลงแบบธรรมชาติ ทำการบรรจุใหม่สิ่งที่อยู่ข้างในที่ไม่ได้ถูกแตะไปยังภาชนะที่ต่างกัน ในลำดับของการกระทำแบบนี้ไม่สำคัญ

เราได้เห็นconeต่างๆในนิยามของlimitแทนที่โดยการแปลงแบบธรรมชาติ ความเป็นธรรมชาติรับรองว่าด้านข้างของทุกๆconeนั้นcommuteกัน แต่limitนั้นถูกนิยามในรูปแบบของการโยงระหว่างcone การโยงแบบนี้ต้องก็บรรลุเงื่อนไขของความเป็นcommute (ตัวอย่างเช่นสามเหลี่ยมต่างๆในนิยามของproductต้องcommute)

เงื่อนไขเหล่านี้ก็อาจจะถูกแทนที่โดยความเป็นธรรมชาติ คุณอาจจะจำได้ว่าconeสากลหรือlimitถูกนิยามในฐานะการแปลงแบบธรรมชาติระหว่างhom-functorแบบ(contravariant)

\[ F :: c \to \textbf{C}(c, \lim D) \]

และก็functorแบบ(contravariant)ที่โยงวัตถุใน\(C\)ไปยังconeที่พวกมันเองคือการแปลงแบบธรรมชาติ

\[ G :: c \to \textbf{Nat}(\Delta_c, D) \]

ในที่นี้\(\Delta_c\)คือfunctorที่คงที่และ\(D\)คือfunctorที่นิยามdiagramใน\(\textbf{C}\) ทั้งสองfunctor\(F\)และ\(G\)มีการกระทำที่ถูกนิยามอย่างถูกต้องบนmorphismใน\(\textbf{C}\) มันเป็นว่าการแปลงแบบธรรมชาติโดยเฉพาะนี้จาก\(F\)ไปยัง\(G\)คือisomorphism

18.4 Isomorphismแบบธรรมชาติ

Isomorphismแบบธรรมชาติ(ที่คือการแปลงแบบธรรมชาติที่ทุกๆส่วนประกอบนั้นสามารถinvertได้) คือวิธีการของทฤษฎีcategoryในการบอกว่า”สองสิ่งนั้นเหมือนกัน” ส่วนประกอบของการแปลงแบบนี้ต้องเป็นisomorphismระหว่างวัตถุ(morphismที่มีinverse) ถ้าคุณนึกภาพimageของfunctorในฐานะแผ่น isomorphismแบบธรรมชาติคือการโยงระหว่างแผ่นเหล่านี้

18.5 Hom-Sets

แต่อะไรคือmorphismต่างๆ พวกมันมีโครงสร้างมากว่าวัตถุคือไม่เหมือนวัตถุ morphismมีด้านจบสองด้าน แต่ถ้าคุณคงไว้ของวัตถุที่เป็นแหล่งและวัตถุเป้าหมาย morphismระหว่างของทั้งสองก่อให้เกิดsetที่หน้าเบื่อ(อย่างน้อยสำหรับcategoryขนาดเล็กแบบlocal) เราสามารถให้ชื่อกับสมาชิกของsetเหล่านี้อย่าง\(f\)หรือ\(g\) ในการแยกแยะตัวหนึ่งไปยังอีกตัวหน่ึง แต่มันคืออะไรโดยจริงๆแล้วที่ทำให้พวมมันแตกต่าง?

ตวามแตกต่างอย่างเป็นเนื้อแท้ระหว่างmorphismต่างๆในhom-setที่ให้มาอยู่มนวิธีการที่พวกมันประกอบกับmorphismอีกตัว(จากhom-setใกล้เคียง) ถ้าได้มีmorphism\(h\)ที่การประกอบกัน(จะเป็นทั้งก่อนและหลัง)กับ\(f\)นั้นแตกต่างกับ\(g\)ในตัวอย่างเช่น

\[ h\circ f\ne h\circ g \]

แล้วเราสามารถ”สังเกต”อย่างตรงๆของความแตกต่างระหว่าง\(f\)และ\(g\)แต่ถึงแม้ถ้าความแตกต่างจะไม่สามารถถูกสังเกตอย่างตรงๆ เราอาจจะใช้functorในการขยายhom-setออกมา functor\(F\)อาจจะโยงmorphismทั้งสองไปยังmorphismที่แตกต่าง

\[ Ff \ne Fg \]

ในcategoryที่อุดมกว่าหที่hom-setใกล้เคียงให้รายเอียดที่ชัดเจนกว่ากับเราอย่าง

\[ \]

ที่ \(h'\)ไม่ได้อยู่ในimageของ\(F\)

18.6 IsomorphismของHom-Set

การสร้างแบบcategoryนั้นขึ้นอยู่กับisomorphismระหหว่างhom-sset แต่เนื่องด้วยhom-setนั้นคือแค่set isomorphicเปล่าๆระหว่างพวมมันไม่ได้บอกอะเรามากนัก สำหรับsetที่มีสมาชิกจำกัด isomorphismแค่บอกว่าพวมมันมีจำนวนสมาชิกเดียวกัน ถ้าsetนั้นมีจำนวนไม่จำกัด cardinalityของพวกมันต้องเท่ากัน แต่isomorphismของhom-setใดๆก็ได้ที่มีความหมายต้องนำการแประกอบกันเข้ามาพิจารณาด้วย และการประกอบกันเกี่ยวพันมากกว่าhom-setหนึ่ง เราต้องนิยามisomorphismที่ครอบคลุมชุดของhom-setทั้งหมด และเราต้องกำหนดให้มีเงื่อนไขของความเข้ากันได้ที่ทำงานร่วมกันกับการประกอบกัน และisomorphismแบบธรรมชาติตรงกันกับคุณสมบัติที่ให้มาอย่างแม่นยำ

แต่อะไรคือisomorphismแบบธรรมชาติของhom-set? ความเป็นธรรมชาติคือคุณสมบัติของการโยงระหว่างfunctorไม่ใช่sset ดังนั้นเรากำลังพูดถึงจริงๆเกี่ยวกับisomorphismแบบธรรมชาติระหว่างfunctorแบบที่มีค่าเป็นhom-set functorเหล่านี้นั้นมากกว่าแค่functorที่มีค่าเป็นset การกระทำของพวกมันบนmorphsimนั้นถูกเกิดมาจากhom-functorที่เหมาะสม morphismนั้นถูดโยงอย่างมาตรฐาน(canonically)ไปยังhom-functorโดนการทั้งการประกอบท่อนหรือหลัง (ตาแต่ความcovarianceชองfunctor)

การembedแบบYonedaคือตัวอย่างหนึ่งของisomorphismแบบนี้ มันโยงhom-setใน\(\textbf{C}\)ไปยังhom-setในcategoryของfunctorและมันก็เป็นธรรมชาติ functorหนึ่งในการembedแบบYonedaคือhom-functorใน\(\textbf{C}\)และอีกตัวหนึ่งโยงวัตถุไปยังsetของการแปลงแยยธรรมชาติระหว่างhom-set

นิยามของlimitนั้นก็คือisomorphismแบบธรรมชาติระหว่างhom-set(ตัวที่สองคือในcategoryของfunctor)

\[ \textbf{C}(c, \lim D) \cong \textbf{Nat}(\Delta_c,D) \]

มันกลับมาเป็นว่าการสร้างของเราคือวัตถุexponentialหรือนั้นของmonoidแบบfreeสามารถถูกเขียนใหม่ในฐานะisomorphismแบบธรรมชาติระหว่างhom-set

สิ่งนี้ไม่ใช่ความบังเอิน เราจะเห็นต่อไปว่าสิ่งเหล่านี้คือแค่ตัวอย่างที่แตกต่างกันของadjunctionที่ก็ถูกนิยามในฐานะisomorphismแบบธรรมชาติของhom-set

18.7 ความไม่สมมาตรของHom-Sets

ได้มีข้อสังเกตที่จะช่วยเราในการเช้าใจadjunction Hom-Setsโดยทั่วไปแล้วนั้นไม่สมมาตร hom-setอย่าง\(\textbf{C}(a,b)\)นั้นมักจะแต่ต่างอย่างมากจากhom-setอย่าง\(\textbf{C}(b,a)\) การแสดงที่พื้นฐานที่สุดของความไม่สมมาตรคือpartial orderที่มองในฐานะcategory ในpartial order morphismจาก\(a\)ไปยัง\(b\)มีตัวตนอยู่ก็ต่อเมื่อ\(a\)นั้นน้อยกว่าหรือเท่ากับ\(b\) ถ้า\(a\)และ\(b\)นั้นแตกต่างกัน แล้วไม่สามารถมีmorphismที่ไปในทิศทางตรงข้าม จาก\(b\)ไปยัง\(a\) ดังนั้นถ้าhom-set\(\textbf{C}(a,b)\)นั้นไม่ว่างที่ในกรณีนี้หมายความว่ามันคือsetที่มีสมาชิกหนึ่ง แล้ว\(\textbf{C}(b,a)\)ต้องว่างนอกเสียจะว่า\(a=b\) ลูกศรของcategoryนี้มีการเคลื่อนที่ชัดเจนในทิศทางหนึ่ง

preorderที่ขึ้นกับความสัมพันธ์ที่มาไม่จำเป็นที่ต้องantisymmetric คือก็มีทิศทาง”แทบทั้งหมด”ยกเว้นวงรอบในบางครั้ง มันสะดวกที่จะคิดถึงcategoryทั่วๆไปในฐานะการgeneralizeของpreorder

preorderนั้นคือcategoryที่บางนั้นคือทุกๆhom-setนั้นเป็นแค่setที่มี่สมาชิกเดียวหรือsetว่าง เราสามารถจินตนาการว่าcategoryทั่วๆไปในฐานะpreorderที่หนา

18.8 โจทย์ท้าทาย

1. ลองพิจารณากรณีที่เสื่อมของเงื่อนไขของความเป็นธรรมชาติและวาดdiagramที่เหมาะสม ตัวอย่างเช่นอะไรจะเกิดขึ้นถ้าfunctor\(F\)หรือ\(G\)โยงทั้งวัตถุ\(a\)และ\(b\)(ส่วนปลายของ\(f::a\rightarrow b\))ไปยังวัตถุเดี่ยวกัน ตัวอย่างเช่น\(Fa=Fb\)หรือ\(Ga=Gb\)? (สังเกตว่าคุณได้coneหรือco-coneในรูปแบบนี้) แล้วพิจารณากรณีจ่างๆที่\(Fa=Ga\)หรือ\(Fb=Gb\) สุดท้ายแล้วถ้าคุณเริ่มด้วยmorphismที่ขมวดบนตนเองอย่าง\(f::a\rightarrow a\)?